⚖️ 删除数对后的最小数组长度

📝 题目描述

​ 给你一个下标从0开始的非递减整数数组nums。

​ 你可以执行以下操作任意次：

• 选择两个下标i和j，满足nums[i] < nums[j]。
• 将nums中下标在i和j处的元素删除。剩余元素按照原来的顺序组成新的数组，下标也重新从0开始编号。

​ 请你返回一个整数，表示执行以上操作任意次后（可以执行0次），nums数组的最小数组长度。

📋 代码模板

java

class Solution {
    public int minLengthAfterRemovals(List<Integer> nums) {

    }
}

typescript

function minLengthAfterRemovals(nums: number[]): number {

}

💡 提示

1. $1\le nums.length\le {10}^5$
2. $1\le nums[i]\le {10}^9$
3. $nums$ 是非递减 数组

🚀 示例

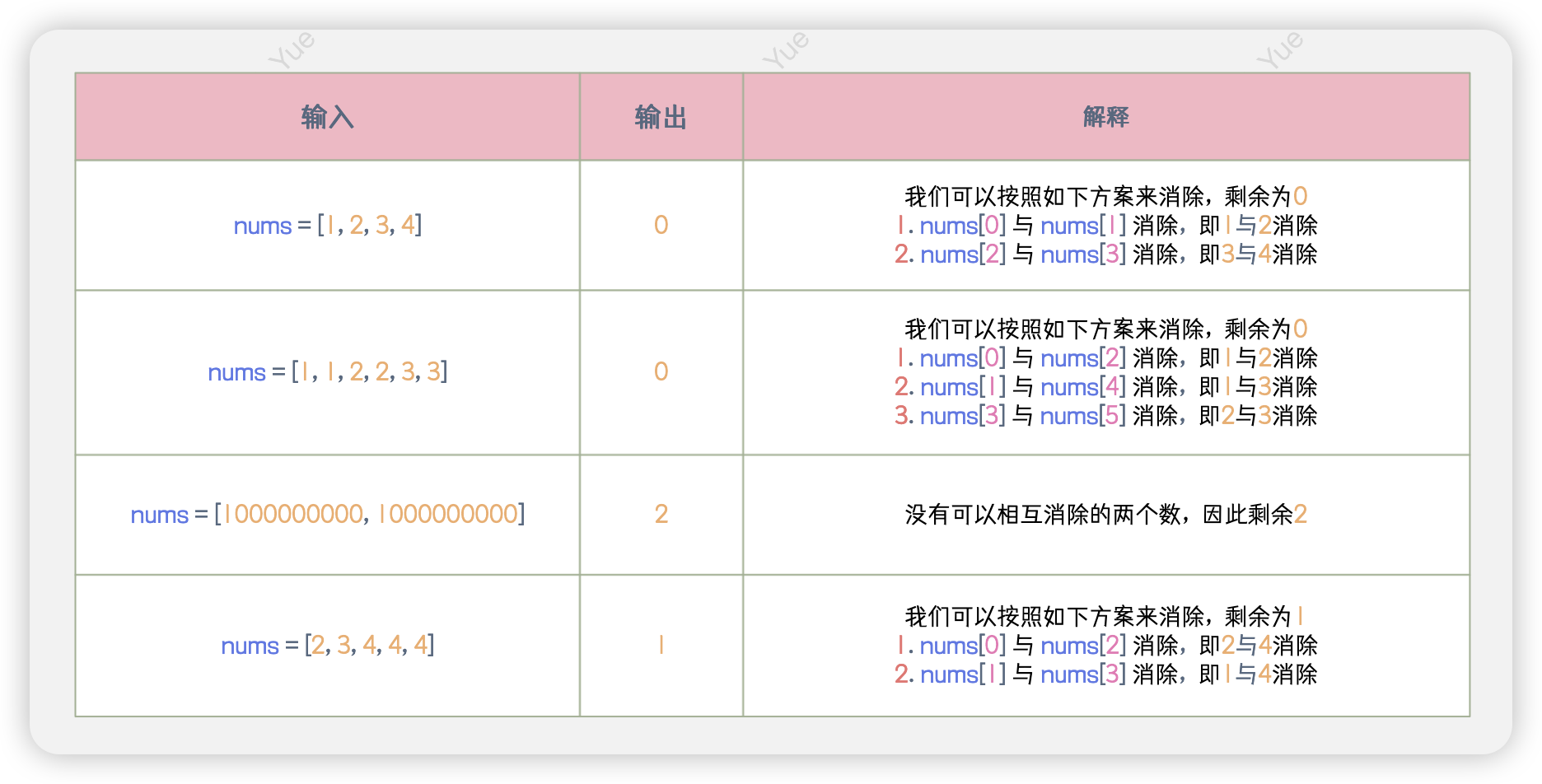
🖊️ 题解

​ 这道题的核心思想是反复对数组中的两个不同数进行相互抵消操作，找出能够剩下的最少数量。

​ 假设 $x$ 出现次数最多，出现次数为 $maxCnt$，我们可以进行如下分类讨论。

• 如果 $maxCnt\cdot 2>n$，其余所有 $n-maxCnt$ 个非 $x$ 数都可以与 $x$ 消除，因此最后剩下 $maxCnt-(n-maxCnt)=2\cdot maxCnt-n$ 个数。
• 如果 $maxCnt\cdot 2\le n$，且 $n$ 是偶数，那么其余数相互消除肯定能剩下 $maxCnt$ 个数，然后再与 $x$ 消除，最后剩下 $0$ 个数。
• 如果 $maxCnt\cdot 2\le n$，且 $n$ 是奇数，同上，最后可以剩下 $1$ 个数。

​ 综上所述，解决本题的关键是求出 $nums$ 中最大的单个数出现次数。我们可以遍历 $nums$ 中的每个数，求出 $maxCnt$。这种方式的时间复杂度为 $O(n)$，那还有没有更快的方式呢？

​ 答案是有的。由于 $nums$ 是有序的，如果 $maxCnt$ 的值超过了 $nums$ 数组长度的一半，那么 $nums[n/2]$ 一定是出现次数最多的那个数，如下图。

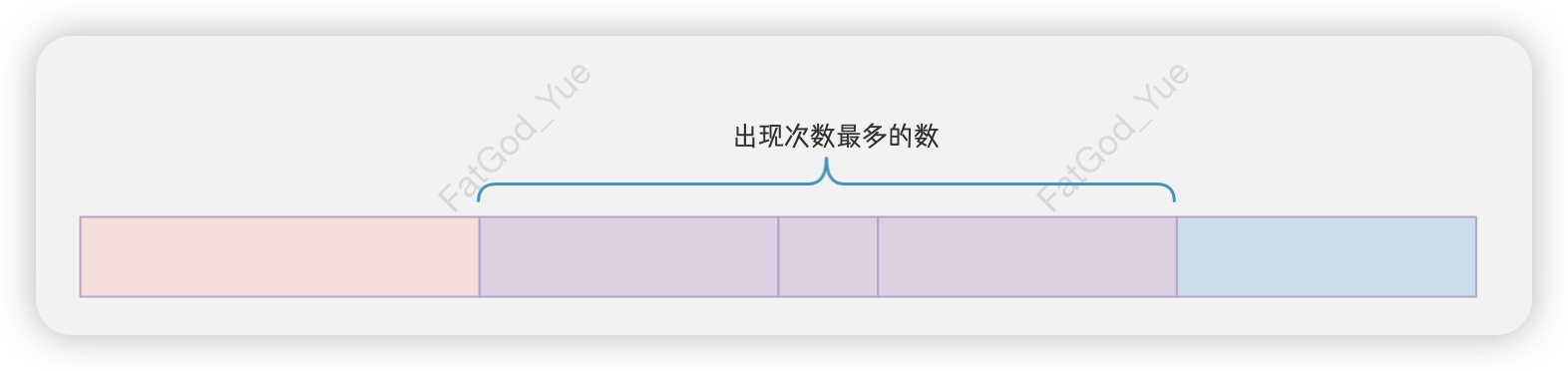
​ 因此我们可以假设 $nums[n/2]$ 是出现次数最多的那个数，并可以利用二分查找得到 $nusms$ 中第一个大于等于 $nums[n/2]$ 的元素下标 $start$，以及第一个大于等于 $nums[n/2+1]$ 的元素下标 $end$，而 $maxCnt$ 的值就等于 $end-start$​。得到 $maxCnt$ 后，可进行如下分类讨论。

• 如果 $maxCnt\cdot 2>n$，那么剩下的数的个数肯定大于 $0$。而在这种情况下 $n\mathrm{mod}2$ 的值最大为 $1$。

• 如果 $maxCnt\cdot 2\le n$，那么剩下的数的个数为 $1$ 或者 $0$。而在这种情况下 $2\cdot maxCnt-n$ 的值肯定 $\le 0$。

​ 可以看到，我们只需要取 $max(2\cdot maxCnt-n,n\mathrm{mod}2)$ 的值，即为答案。

java

class Solution {
    public int minLengthAfterRemovals(List<Integer> nums) {
        int n = nums.size();
        int x = nums.get(n / 2);
        int maxCnt = binarySearch(nums, x + 1) - binarySearch(nums, x);
        return Math.max(2 * maxCnt - n, n % 2);
    }

    private int binarySearch(List<Integer> nums, int target) {
        int low = 0, high = nums.size() - 1;
        while (low <= high) {
            int mid = low + ((high - low) >> 1);
            if (nums.get(mid) >= target) {
                high = mid - 1;
            } else {
                low = mid + 1;
            }
        }
        return low;
    }
}

typescript

function minLengthAfterRemovals(nums: number[]): number {
    const n = nums.length;
    const binarySearch = (target: number): number => {
        let low = 0, high = n - 1;
        while (low <= high) {
            const mid = low + Math.floor((high - low) / 2);
            if (nums[mid] >= target) {
                high = mid - 1;
            } else {
                low = mid + 1;
            }
        }
        return low;
    }
    const x = nums[Math.floor(n / 2)];
    const maxCnt = binarySearch(x + 1) - binarySearch(x);
    return Math.max(2 * maxCnt - n, n % 2);
}

💭 复杂度分析

​ 基于二分查找的解决方案的复杂度分析如下。

• 时间复杂度：$O(\log n)$。其中 $n$ 为 $nums.length$。
• 空间复杂度：$O(1)$。