📋 你可以安排的最多任务数目

📝 题目描述

​ 给你n个任务和m个工人。每个任务需要一定的力量值才能完成，需要的力量值保存在下标从0开始的整数数组tasks中，第i个任务需要tasks[i]的力量才能完成。每个工人的力量值保存在下标从0开始的整数数组workers中，第j个工人的力量值为workers[j]。每个工人只能完成一个任务，且力量值需要大于等于该任务的力量要求值（即workers[j] >= tasks[i]）。

​ 除此之外，你还有pills个神奇药丸，可以给一个工人的力量值增加strength。你可以决定给哪些工人使用药丸，但每个工人最多只能使用一片药丸。

​ 给你下标从0开始的整数数组tasks和workers以及两个整数pills和strength，请你返回最多有多少个任务可以被完成。

📋 代码模板

java

class Solution {
    public int maxTaskAssign(int[] tasks, int[] workers, int pills, int strength) {

    }
}

typescript

function maxTaskAssign(tasks: number[], workers: number[], pills: number, strength: number): number {
    
}

💡 提示

1. $n=tasks.length$
2. $m=workers.length$
3. $1\le n\le 5\cdot {10}^4$
4. $1\le m\le 5\cdot {10}^4$​
5. $0\le pills\le m$
6. $0\le tasks[i]\le {10}^9$
7. $0\le workers[i]\le {10}^9$
8. $0\le strength\le {10}^9$

🚀 示例

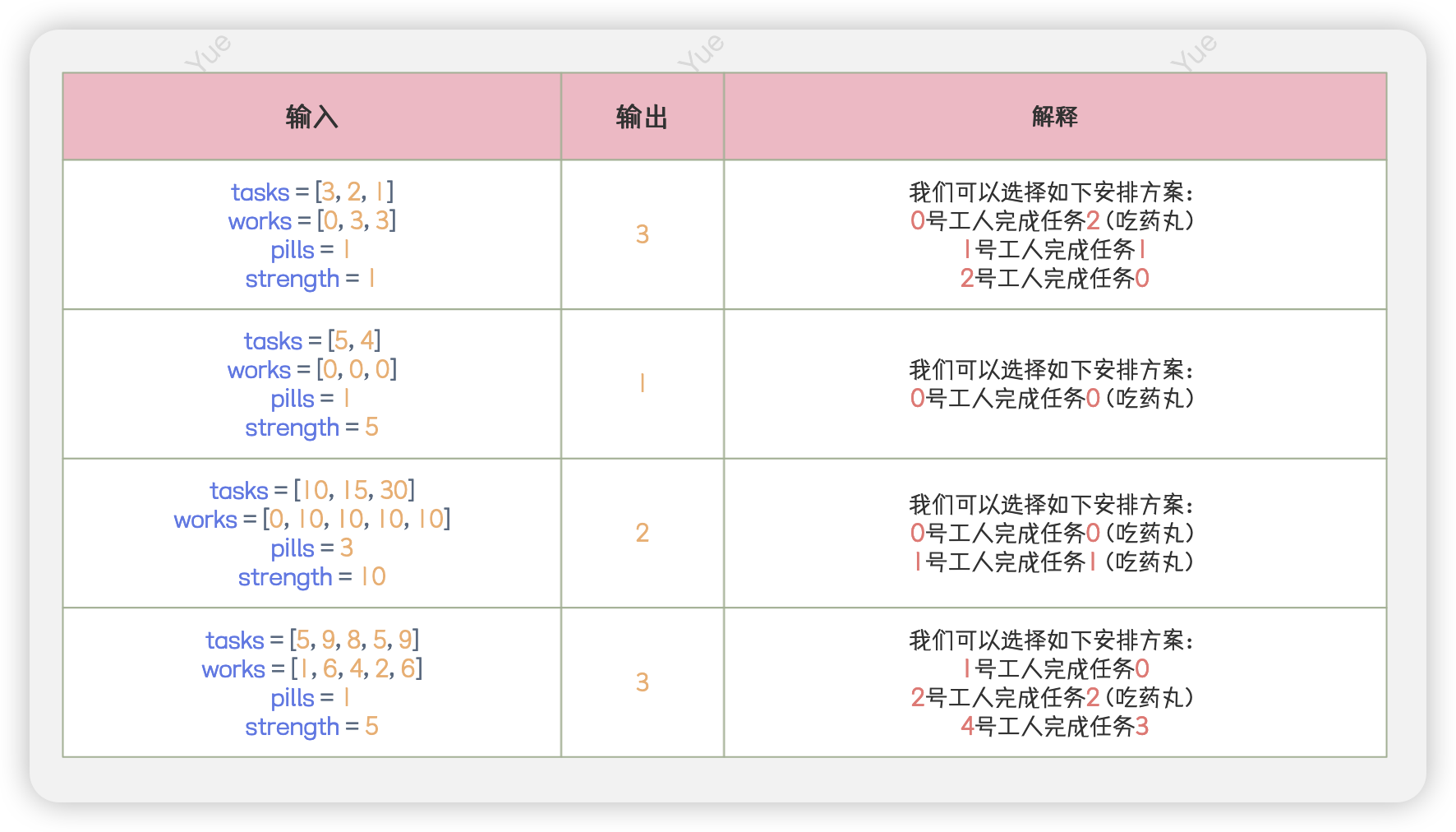
🖊️ 题解

二分查找

​ 假设工人们能够完成 $k$ 个任务，那么他们一定能够完成 $<k$ 个任务，相反，如果工人们不能够完成 $k$ 个任务，那么也一定不能够完成 $>k$ 个任务。根据该单调性，我们可以利用二分查找来得到工人们能够完成的最大任务数 $answer$。

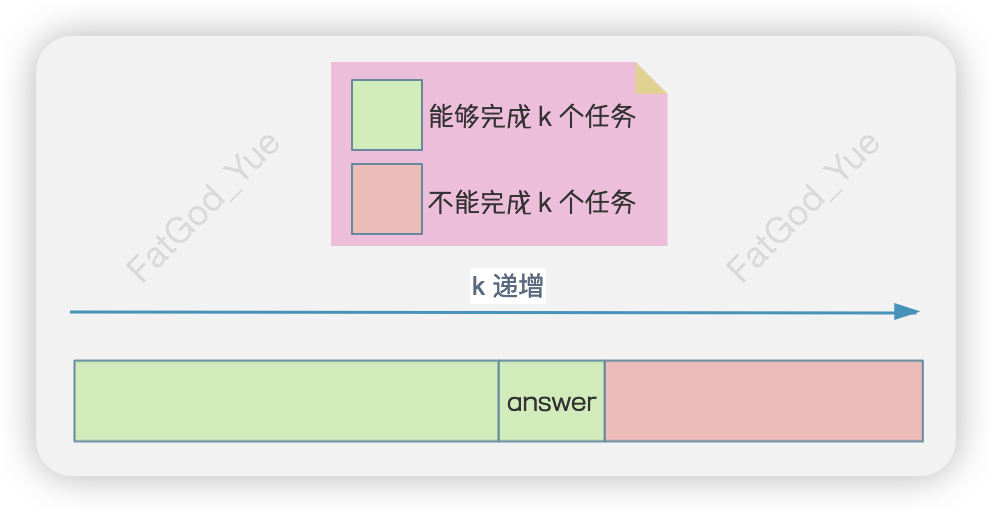
​ 二分查找的下限可以设置为 $1$，这是因为在存在任务完成的前提下，$1$ 是最小任务数。而二分查找的上限可以设置为 $min(m,n)$，这是因为每个工人只能完成一个任务，一个任务只能被完成一次。

​ 那么我们如何来验证工人们是否能够完成 $k$ 个任务呢？为此，我们可以进行贪心选择，即选择力量值最大的 $k$ 个工人和所需力量值最小的 $k$ 个任务，并判断这 $k$ 个工人是否能够把这 $k$ 个任务都完成，如果都能够完成，则说明工人们能够完成 $k$ 个任务；否则，工人们不能够完成 $k$​ 个任务。

​ 为了判断力量值最大的 $k$ 个工人是否能够全部完成所需力量值最小的 $k$ 个任务，我们可以优先选择所需力量值最大的任务分配给工人，此时将会出现以下两种情况：

1. 有工人的力量值大于等于该任务的所需力量值，设他们为 $cans$，那么我们不能浪费药丸，即不使用药丸。同时，让 $cans$ 中力量值最大的工人来完成该任务，这是因为 $cans$ 中的任意一个工人都能够完成剩余的任一任务，无论挑选哪个工人来完成该任务，都不会影响后续任务的完成。
2. 所有工人的力量值都小于该任务的所需力量值，那么我们必须挑选一名工人并使用药丸来完成该任务，前提为：其服用药丸后的力量值需大于等于该任务的所需力量值。假设满足这个前提的工人集合为 $cans$，我们需让 $cans$ 中自身（不服用药丸）力量值最小的工人来完成该任务，这是因为 $cans$​ 中任意一个工人在服用药丸后，都能够完成剩余的任一任务，无论挑选哪个工人来完成该任务，都不会影响后续任务的完成。

​ 综上所述，我们可以使用一个有序集合 $wks$，按照工人的力量值，从小到大维护挑选的工人。并且按照任务的所需力量值，从大到小枚举挑选的每一个任务，对于每个任务 $tasks[i]$ ：

1. 如果有序集合 $wks$ 中最大的元素大于等于 $task[i]$，那么将最大的元素从有序集合 $wks$ 中删除，并进入下一轮任务枚举。
2. 如果有序集合 $wks$ 中最大的元素小于 $task[i]$，那么此时若没有药丸剩余或者有序集合中不存在大于等于 $t-strength$ 的元素，则说明我们就无法完成所有任务，可直接停止枚举，返回false；相反，该任务能够被完成，删除有序集合 $wks$ 中第一个大于等于 $t-strength$ 的元素（这个过程可使用二分查找）。

java

class Solution {
    public int maxTaskAssign(int[] tasks, int[] workers, int pills, int strength) {
        Arrays.sort(tasks);
        Arrays.sort(workers);
        int low = 1, high = Math.min(tasks.length, workers.length);
        while (low <= high) {
            int mid = low + ((high - low) >> 1);
            if (check(tasks, workers, pills, strength, mid)) {
                low = mid + 1;
            } else {
                high = mid - 1;
            }
        }
        return high;
    }

    private boolean check(int[] tasks, int[] works, int pills
            , int strength, int k) {
        int m = works.length;
        List<Integer> wks = new ArrayList<>();
        for (int i = m - k; i < m; i++) {
            wks.add(works[i]);
        }
        for (int i = k - 1; i >= 0; i--) {
            int last = wks.size() - 1;
            if (wks.get(last) >= tasks[i]) {
                wks.remove(last);
                continue;
            }
            if (pills <= 0) {
                return false;
            }
            int index = binarySearch(wks, tasks[i] - strength);
            if (index == wks.size()) {
                return false;
            }
            pills--;
            wks.remove(index);
        }
        return true;
    }

    private int binarySearch(List<Integer> nums, int target) {
        int low = 0, high = nums.size() - 1;
        while (low <= high) {
            int mid = low + ((high - low) >> 1);
            if (nums.get(mid) >= target) {
                high = mid - 1;
            } else {
                low = mid + 1;
            }
        }
        return low;
    }
}

typescript

function maxTaskAssign(tasks: number[], workers: number[], pills: number, strength: number): number {
    tasks.sort((n1, n2) => n1 - n2);
    workers.sort((n1, n2) => n1 - n2);
    const binarySearch = (nums: number[], target: number): number => {
        let low = 0, high = nums.length - 1;
        while (low <= high) {
            const mid = low + Math.floor((high - low) / 2);
            if (nums[mid] >= target) {
                high = mid - 1;
            } else {
                low = mid + 1;
            }
        }
        return low;
    }
    const check = (k: number, pills: number): boolean => {
        const m = workers.length;
        const wks: number[] = [];
        for (let i = m - k; i < m; i++) {
            wks.push(workers[i]);
        }
        for (let i = k - 1; i >= 0; i--) {
            const last = wks.length - 1;
            if (wks[last] >= tasks[i]) {
                wks.splice(last, 1);
                continue;
            }
            if (pills <= 0) {
                return false;
            }
            const index = binarySearch(wks, tasks[i] - strength);
            if (index == wks.length) {
                return false;
            }
            pills--;
            wks.splice(index, 1);
        }
        return true;
    }
    let low = 1, high = Math.min(tasks.length, workers.length);
    while (low <= high) {
        const mid = low + Math.floor((high - low) / 2);
        if (check(mid, pills)) {
            low = mid + 1;
        } else {
            high = mid - 1;
        }
    }
    return high;
}

二分查找 + 双端队列

​ 在以上算法中，虽然删除有序集合 $wks$ 中最大元素的时间复杂度为常数级别，但利用二分查找来删除有序集合 $wks$ 中第一个大于等于 $task[i]-strength$ 的元素的时间复杂度为对数级别。那有什么好的办法来降低删除工人元素的时间复杂度吗？

​ 可以发现，对于当前任务的一次枚举中，如果存在多个大于等于 $task[i]-strength$ 的元素，由于任务的枚举是从大到小的，只要存在充足的药丸，这些元素对应的工人就一定能够完成后续的任务。因此，在每一次枚举中，我们可以将这些大于等于 $task[i]-strength$​ 的元素按照从小到大的顺序，保存在一个双端队列中，并在其中选择一个合适的元素进行删除，具体做法为：

1. 若双端队列中不存在元素，则说明，对于当前任务，即使在服用药丸后，也没有工人能够完成该任务，此时可提前结束枚举，并返回false。

2. 若最大元素大于等于 $task[i]$，不需要使用药丸，将其删除后进入下一轮枚举。

3. 若最大元素小于 $task[i]$，则使用一颗药丸，并删除最小元素。需要注意的是，这个过程可能已经没有药丸可供使用，此时也应提前结束枚举，并返回false。

​ 根据上述内容，可以得出：维护双端队列来替代有序集合，可以使删除工人元素的时间复杂度从 $O(logk)$ 降低为 $O(1)$。

java

class Solution {
    public int maxTaskAssign(int[] tasks, int[] workers, int pills, int strength) {
        Arrays.sort(tasks);
        Arrays.sort(workers);
        int low = 1, high = Math.min(tasks.length, workers.length);
        while (low <= high) {
            int mid = low + ((high - low) >> 1);
            if (check(tasks, workers, pills, strength, mid)) {
                low = mid + 1;
            } else {
                high = mid - 1;
            }
        }
        return high;
    }

    private boolean check(int[] tasks, int[] works, int pills
            , int strength, int k) {
        int m = works.length;
        Deque<Integer> deque = new LinkedList<>();
        int cursor = m - 1;
        for (int i = k - 1; i >= 0; i--) {
            while (cursor >= m - k && works[cursor] + strength >= tasks[i]) {
                deque.addFirst(works[cursor]);
                cursor--;
            }
            if (deque.isEmpty()) {
                return false;
            }
            if (deque.getLast() >= tasks[i]) {
                deque.removeLast();
                continue;
            }
            if (pills <= 0) {
                return false;
            }
            pills--;
            deque.removeFirst();
        }
        return true;
    }
}

typescript

function maxTaskAssign(tasks: number[], workers: number[], pills: number, strength: number): number {
    tasks.sort((n1, n2) => n1 - n2);
    workers.sort((n1, n2) => n1 - n2);
    const check = (k: number, pills: number): boolean => {
        const m = workers.length;
        const deque: Deque<number> = new LinkedListDeque();
        let cursor = m - 1;
        for (let i = k - 1; i >= 0; i--) {
            while (cursor >= m - k && workers[cursor] + strength >= tasks[i]) {
                deque.pushFirst(workers[cursor]);
                cursor--;
            }
            if (deque.isEmpty()) {
                return false;
            }
            const last = deque.size() - 1;
            if (deque.peekLast()! >= tasks[i]) {
                deque.popLast();
                continue;
            }
            if (pills <= 0) {
                return false;
            }
            pills--;
            deque.popFirst();
        }
        return true;
    }
    let low = 1, high = Math.min(tasks.length, workers.length);
    while (low <= high) {
        const mid = low + Math.floor((high - low) / 2);
        if (check(mid, pills)) {
            low = mid + 1;
        } else {
            high = mid - 1;
        }
    }
    return high;
}

interface Deque<T> {
    pushLast(val: T): void;

    pushFirst(val: T): void;

    popLast(): T | null;

    popFirst(): T | null;

    peekLast(): T | null;

    peekFirst(): T | null;

    size(): number;

    isEmpty(): boolean;
}

class LNode<T> {
    prev: LNode<T> | null = null;
    next: LNode<T> | null = null;
    val: T;

    constructor(val: T) {
        this.val = val;
    }
}

class LinkedListDeque<T> implements Deque<T> {
    private front: LNode<T> | null = null;
    private rear: LNode<T> | null = null;
    private queueSize: number;

    constructor() {
        this.queueSize = 0;
    }

    pushLast(val: T): void {
        const node = new LNode(val);
        if (this.isEmpty()) {
            this.front = this.rear = node;
        } else {
            this.rear!.next = node;
            node.prev = this.rear;
            this.rear = node;
        }
        this.queueSize++;
    }

    pushFirst(val: T): void {
        const node = new LNode(val);
        if (this.isEmpty()) {
            this.front = this.rear = node;
        } else {
            this.front!.prev = node;
            node.next = this.front;
            this.front = node;
        }
        this.queueSize++;
    }

    popLast(): T | null {
        if (this.isEmpty()) {
            return null;
        }
        const value: T = this.rear!.val;
        let temp: LNode<T> | null = this.rear!.prev;
        if (temp) {
            temp.next = null;
            this.rear!.prev = null;
        }
        this.rear = temp;
        this.queueSize--;
        return value;
    }

    popFirst(): T | null {
        if (this.isEmpty()) {
            return null;
        }
        const value: T = this.front!.val;
        let temp: LNode<T> | null = this.front!.next;
        if (temp) {
            temp.prev = null;
            this.front!.next = null;
        }
        this.front = temp;
        this.queueSize--;
        return value;
    }

    peekLast(): T | null {
        return this.isEmpty() ? null : this.rear!.val;
    }

    peekFirst(): T | null {
        return this.isEmpty() ? null : this.front!.val;
    }

    size(): number {
        return this.queueSize;
    }

    isEmpty(): boolean {
        return this.queueSize == 0;
    }
}

💭 复杂度分析

​ 基于二分查找的解决方案的复杂度分析如下。

• 时间复杂度：$O(n\log n+m\log m+\log C\ast k\ast \log k)$，其中 $n=tasks.length,m=workers.length,C=min(m,n)$，$n\log n$ 为对数组 $tasks$ 排序所需的时间复杂度，$m\log m$ 为对数组 $workers$ 排序所需的时间复杂度。而 $\log C\ast k\ast \log k$ 为二分查找答案的时间复杂度。
• 空间复杂度：$O(\log n+\log m+C)$。其中 $\log n$ 为对数组 $tasks$ 排序所需要的栈的空间复杂度，$\log m$ 为对数组 $workers$ 排序所需要的栈的空间复杂度，$C$ 为二分查找所需要的有序集合的空间复杂度。

​ 基于二分查找 + 双端队列的解决方案的复杂度分析如下。

• 时间复杂度：$O(n\log n+m\log m+k\log C)$。
• 空间复杂度：$O(\log n+\log m+C)$。