💻 同时运行 N 台电脑的最长时间

📝 题目描述

​ 你有n台电脑。给你整数n和一个下标从0开始的整数数组batteries，其中第i个电池可以让一台电脑运行batteries[i]分钟。你想使用这些电池让全部n台电脑同时运行。

​ 一开始，你可以给每台电脑连接至多一个电池。然后在任意整数时刻，你都可以将一台电脑与它的电池断开连接，并连接另一个电池，你可以进行这个操作任意次。新连接的电池可以是一个全新的电池，也可以是别的电脑用过的电池。断开连接和连接新的电池不会花费任何时间。

​ 注意，你不能给电池充电。

​ 请你返回你可以让n台电脑同时运行的最长分钟数。

📋 代码模板

java

class Solution {
    public long maxRunTime(int n, int[] batteries) {

    }
}

typescript

function maxRunTime(n: number, batteries: number[]): number {
    
}

💡 提示

1. $1\le n\le batteries.length\le {10}^5$
2. $1\le batteries[i]\le {10}^9$

🚀 示例

示例一

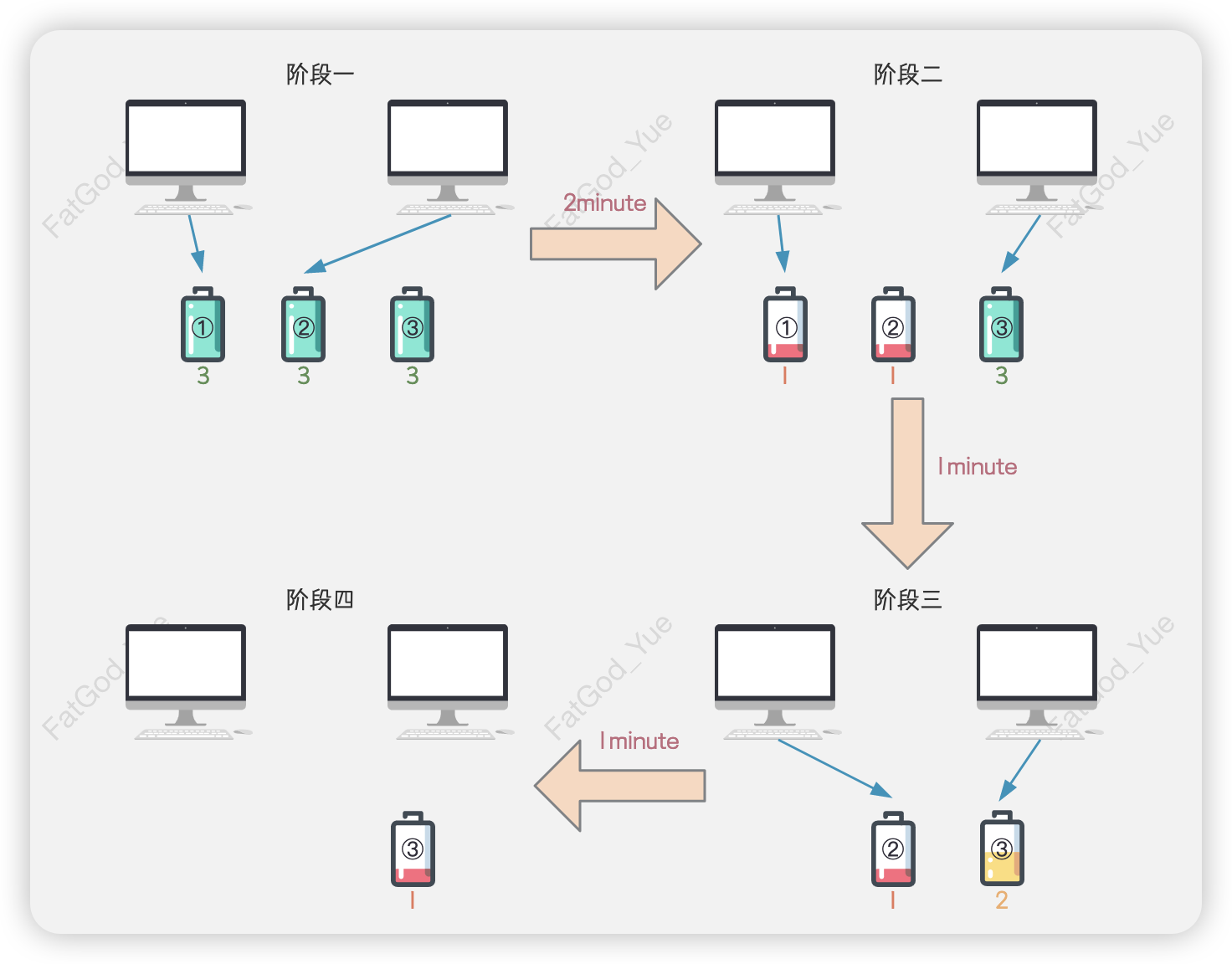
​ 输入为n = 2, batteries = [3,3,3]，输出为4，方案如下。

1. 一开始，将第一台电脑与电池①连接，第二台电脑与电池②连接。
2. $2$ 分钟后，将第二台电脑与电池②断开连接，并连接电池③，此时电池②还可供电 $1$ 分钟。
3. $1$​ 分钟后，将第一台电脑与电池①断开连接，并连接电池②，此时电池①已被耗尽，电池③还可供电 $2$ 分钟。
4. $1$ 分钟后，电池①被耗尽，只剩余电池③可供电 $1$ 分钟，已无法再使两台电脑同时运行。

示例二

​ 输入为n = 2, batteries = [1,1,1,1]，输出为2，方案如下。

1. 一开始，将第一台电脑与电池①连接，第二台电脑与电池③连接。
2. $1$ 分钟后，将第一台电脑与电池①断开连接，并连接电池②。同时，将第二台电脑与电池③断开连接，并连接电池④。此时电池①和③已被耗尽。
3. $1$ 分钟后，电池②和④也被耗尽，无剩余电池可供电，已无法再使两台电脑同时运行。

🖊️ 题解

​ 假设 $n$ 台电脑能够同时运行 $t$ 分钟，那么它们也一定能够同时运行 $<t$ 分钟，相反，如果 $n$ 台电脑不能同时运行 $t$ 分钟，那么它们也一定不能同时运行 $>t$ 分钟。根据该单调性，本题可以利用二分查找来得到 $n$ 台电脑能够同时运行的最长时间 $answer$​。

​ 二分查找的下限可以设置为 $1$，这是因为 $1$ 是 $n$ 台电脑能够同时运行的最小分钟。而二分查找的上限可以设置为 $\lfloor \frac{\sum _{i=0}^{n-1}batteries[i]}{n}\rfloor ,n=batteries.length$，这是因为答案不可能超过电池电量和 $\sum _{i=0}^{n-1}batteries[i]$ 除以电脑数量 $n$​（向下取整）。

​ 那么我们如何来验证所有电脑是否能够同时运行 $t$ 分钟呢？在 $t$ 分钟内，如果一块电池的电量超过 $t$，那它最多也只能被使用 $t$ 分钟，因此对于每一块电池，其在 $t$ 分钟内能够使用的电量分钟数为 $min(t,batteries[i])$ 。我们把所有电池能够使用的电量分钟数加起来，记作 $sum$，即 $sum=\sum _{i=0}^{n-1}min(t,batteries[i])$，而 $check$ 函数为真的条件就是 $sum\ge n\cdot t$​，论证方法如下。

• 设 $n$ 为 $4$，$t$ 为 $6$，$batteries$ 为 $[7,4,5,3,6]$，验证这 $4$ 台电脑能否同时运行 $6$ 分钟。

• 要使 $n$ 台电脑同时运行 $t$ 分钟，需要 $n\cdot t$ 格电量，我们可以把它类比为一个 $t\cdot n$ 的网格，每个单元格为所需的一格电量。

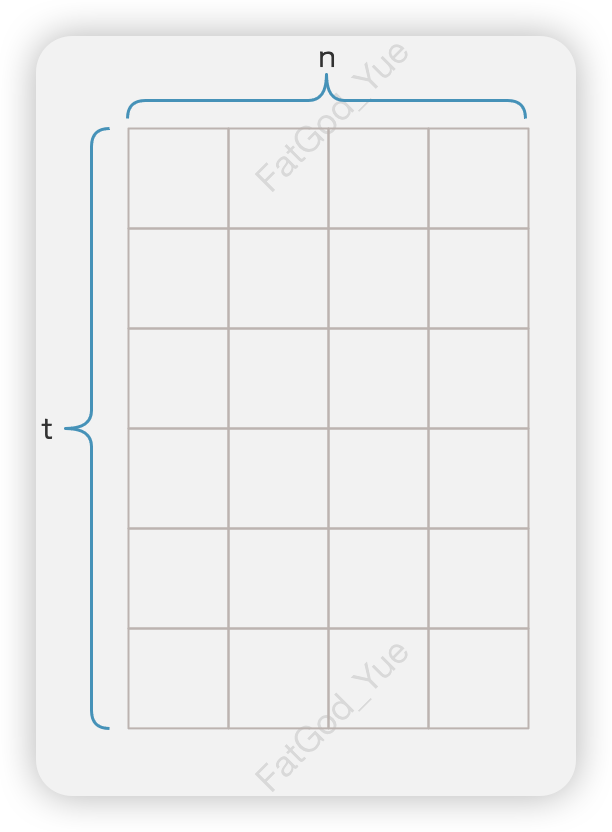
• 我们把不同电池的电量用不同颜色进行标记，从每块电池选取 $min(t,batteries[i])$ 格电量，共 $sum$ 格电量。

• 按颜色交替地列式涂色 $t\cdot n$ 的网格，若能涂色满，则说明 $n$ 台电脑能够同时运行 $t$ 分钟，否则 $n$ 台电脑不能够同时运行 $t$ 分钟。因此，将网格涂满色的条件为 $sum\ge t\cdot n$，也是 $check$ 函数为真的条件。其中，每一行代表一分钟。

• 题目要求同一块电池在同一分钟内只能被一台电脑使用，即说明一行中的单元格不能出现相同涂色，那上述涂色法就一定能够保证这一点成立呢？答案是能够保证，因为一列上的单元格数量为 $t$​，在这种涂色方案下，对于任意一个涂色的单元格，如果要在其所在行上出现相同的涂色，颜色的数量至少需要 $t+1$ 个，而一个相同的颜色的选择数量最大为 $t$​，所以在同一行上不可能出现相同的涂色。

java

class Solution {
    public long maxRunTime(int n, int[] batteries) {
        long total = 0;
        for (int battery : batteries) {
            total += battery;
        }
        long low = 1, high = total / n;
        while (low <= high) {
            long mid = low + ((high - low) >> 1);
            if (check(n, batteries, mid)) {
                low = mid + 1;
            } else {
                high = mid - 1;
            }
        }
        return high;
    }

    private boolean check(int n, int[] batteries, long t) {
        long sum = 0;
        for (int battery : batteries) {
            sum += Math.min(battery, t);
        }
        return n * t <= sum;
    }
}

typescript

function maxRunTime(n: number, batteries: number[]): number {
    const check = (t: number): boolean => {
        let sum = 0;
        for (const battery of batteries) {
            sum += Math.min(battery, t);
        }
        return n * t <= sum;
    }
    let low = 1, high = Math.floor(batteries.reduce((acc, cur) => acc + cur, 0) / n);
    while (low <= high) {
        const mid = low + Math.floor((high - low) / 2);
        if (check(mid)) {
            low = mid + 1;
        } else {
            high = mid - 1;
        }
    }
    return high;
}

💭 复杂度分析

​ 基于二分查找的解决方案的复杂度分析如下。

• 时间复杂度：$O(n\log C)$，其中 $C$ 为二分查找的上下限之差，$n$ 为数组 $batteries$ 长度。
• 空间复杂度：$O(1)$。