🪐 小行星碰撞

📝 题目描述

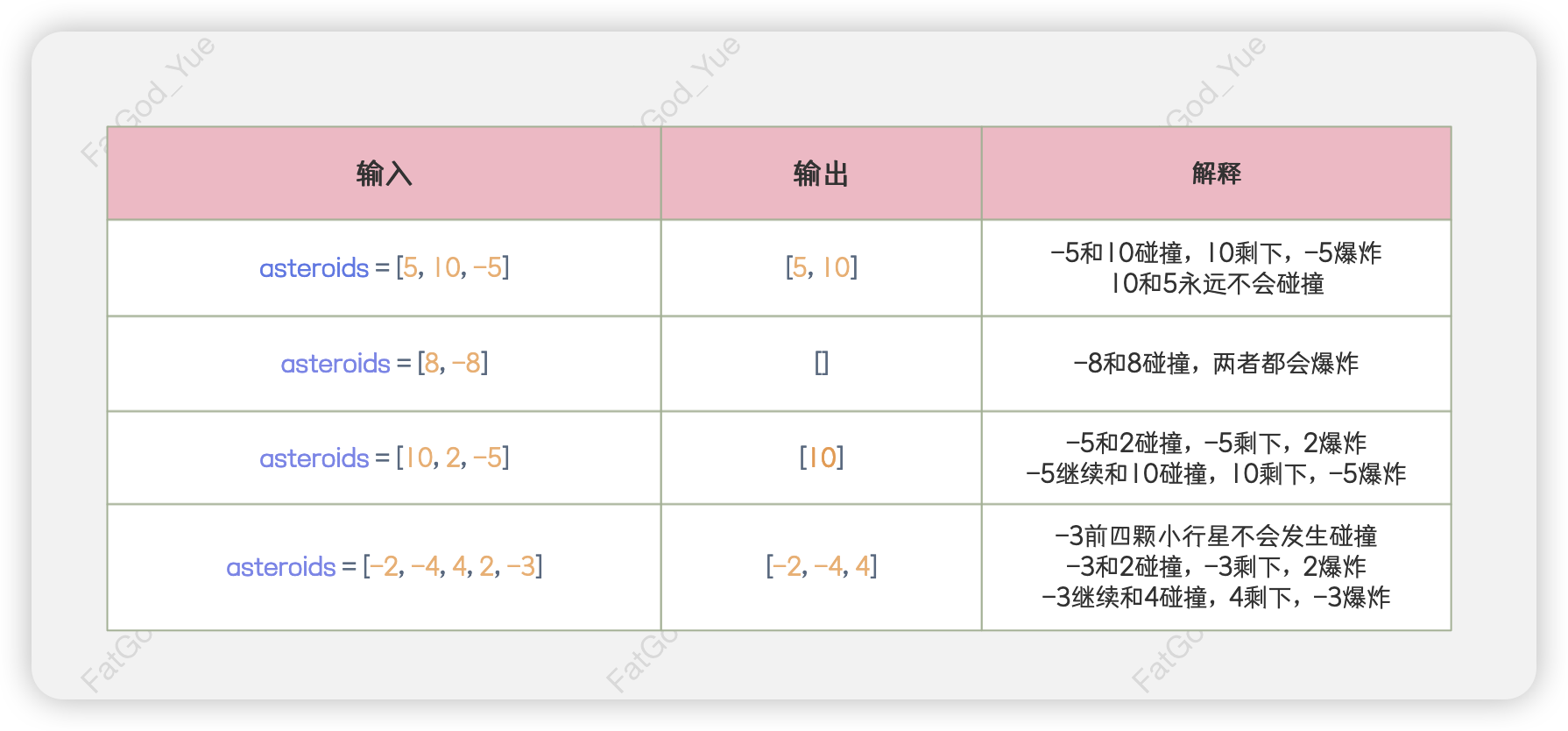
​ 给定一个非0整数数组asteroids，表示在同一行的小行星。

​ 对于数组中的每一个元素，其绝对值表示小行星的大小，正负表示小行星的移动方向（+表示向右移动，-表示向左移动）。例如，-5代表小行星的大小为5，且向左移动。

​ 在同一行上的小行星的移动速度都是相同的，但它们可能会发生碰撞，碰撞规则如下。

1. 当两颗小行星相互碰撞时，较小的小行星会爆炸。
2. 当两颗小行星相互碰撞时，若它们的大小相同，则两个小行星都会爆炸。
3. 两颗移动方向相同的小行星，永远不会发生碰撞。

​ 请你找出在碰撞后，asteroids中剩下的所有小行星。

📋 代码模版

class Solution {
    public int[] asteroidCollision(int[] asteroids) {

    }
}

💡 提示

1. $2<=asteroids.length<={10}^4$
2. $-1000<=asteroids[i]<=1000$
3. $asteroids[i]\ne 0$

🚀 示例

🖊️ 题解

​ 以下是两颗小行星在四种移动场景下是否会发生碰撞的情况。在第二和第三种移动场景中，由于两颗小行星的移动方向和速度相同，因此它们不会发生碰撞。在第一种移动场景中，两颗小行星虽然朝着不同的方向进行移动，但它们相距只会越来越远，因此它们也不会发生碰撞。

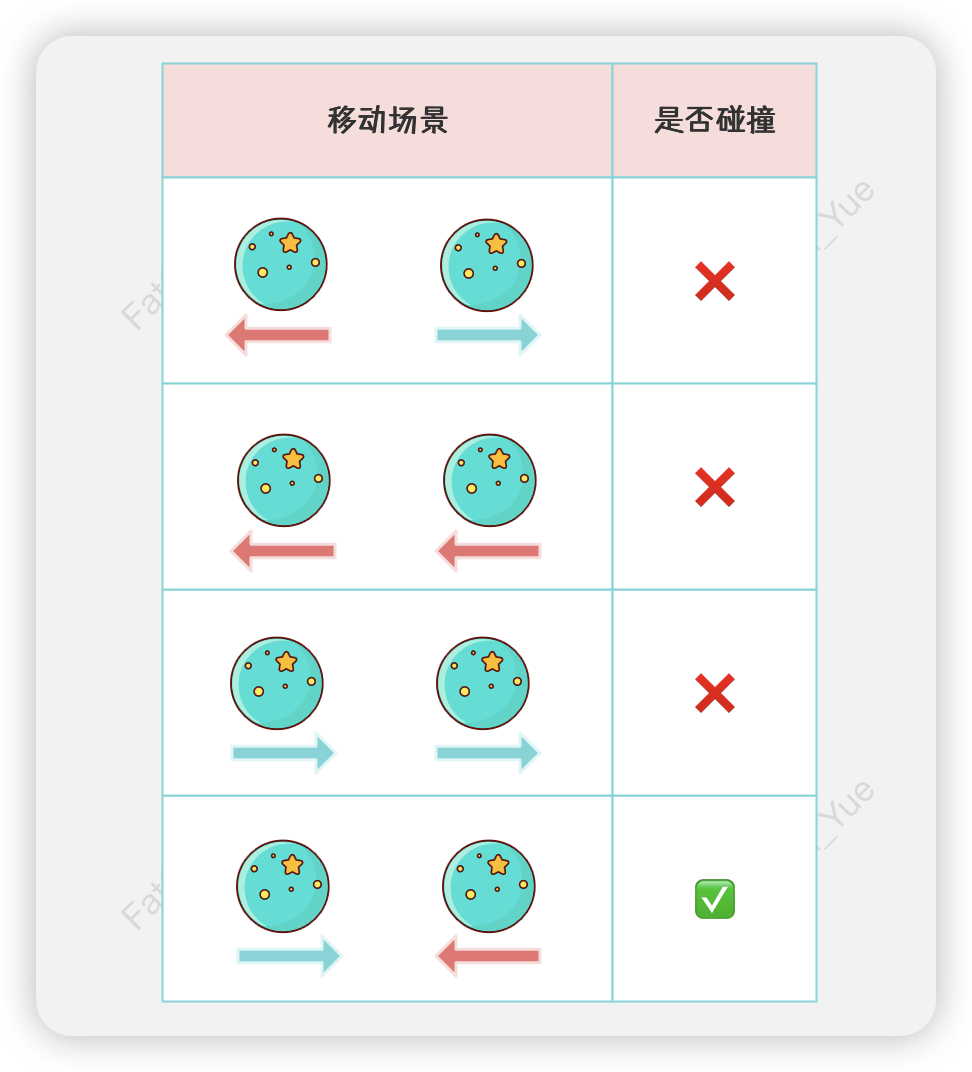
​ 由上图可知，仅当一颗向左移动的小行星（负-）遇到一颗向右移动的小行星（正+）时，两者才会发生碰撞。需要注意的是，一颗向左移动的小行星在与向右移动的小行星碰撞存活后，其可能还会与其他向右移动的小行星碰撞。

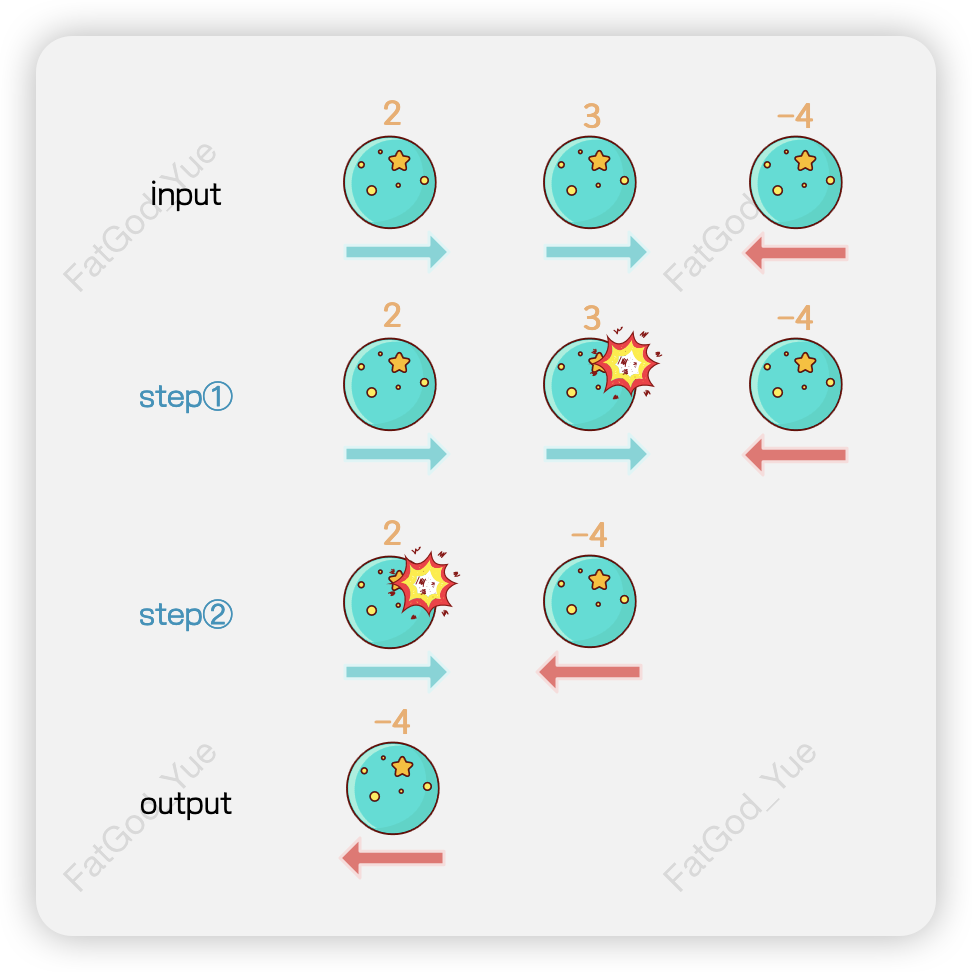
​ 综上所述，该题可以使用「栈」这一数据结构来模拟解决，具体步骤下。

1. 创建一个栈，用于存放小行星表示的数字。
2. 遍历的给定的小行星数组asteroids，在每一轮遍历中，只有当当前小行星asteroid向左移动（负数）且栈顶小行星向右移动（正数）时，才进行碰撞操作，其它情况下，应直接将当前小行星压入栈中。在这种特殊情况下，可能存在边界问题，即栈顶小行星不存在（栈为空），此时也应直接将当前小行星压入栈中。需要注意的是，一个向左移动（负数）的小行星可能会引发连续碰撞，因此碰撞过程应为一次循环。向左移动（负数）的小行星在碰撞过程中，可能会存活下来，也可能会爆炸，所以在碰撞过程前需记录一个布尔标记alive表示当前向左移动（负数）的小行星是否存活。由于当前小行星爆炸后应结束碰撞，alive也将用作碰撞循环的条件。若在碰撞结束后，若alive仍为true，则将当前小行星压入栈中。在每一轮碰撞中，需更新当前小行星的alive的值，并根据两颗小行星的大小比较判断栈顶的元素是否会爆炸，如果发生爆炸，则弹出栈顶的小行星元素。
3. 将辅助栈中剩余的元素自顶向底组装成一个整形数组返回。

​ ⭐️由于alive初始化为true，且其它情况不会进入碰撞循环，而是直接将元素压入栈中。因此，在其它情况下，当前小行星的存活状态也可用alive表示，它的值不会被更新，即值永远为true。

class Solution {
    public int[] asteroidCollision(int[] asteroids) {
        Deque<Integer> stack = new ArrayDeque<>();
        for (int asteroid : asteroids) {
            boolean alive = true;
            while (alive && asteroid < 0 && !stack.isEmpty() && stack.peek() > 0) {
                alive = -asteroid > stack.peek();
                if (stack.peek() <= -asteroid) {
                    stack.pop();
                }
            }
            if (alive) {
                stack.push(asteroid);
            }
        }
        int[] result = new int[stack.size()];
        for (int i = stack.size() - 1; i >= 0; i--) {
            result[i] = stack.pop();
        }
        return result;
    }
}

💭 复杂度分析

​ 基于栈 + 模拟的解决方案的复杂度分析如下。

• 时间复杂度：$O(n)$，其中$n$为小行星数组长度。
• 空间复杂度：$O(n)$ 。