📍 在排序数组中查找元素的第一个和最后一个位置

📝 题目描述

​ 给你一个按照非递减（递增）顺序排列的整数数组nums，和一个目标值target，请你找出给定目标值在数组中的开始位置和结束位置。

​ 如果数组中不存在目标值target，返回[-1, -1]。

​ 你必须设计并实现时间复杂度为0(log n)的算法解决此问题。

📋 代码模版

java

class Solution {
    public int[] searchRange(int[] nums, int target) {

    }
}

typescript

function searchRange(nums: number[], target: number): number[] {
    
}

💡 提示

1. $0\le nums.length\le {10}^5$
2. ${-10}^9\le nums[i]\le {10}^9$
3. ${-10}^9\le target\le {10}^9$

🚀 示例

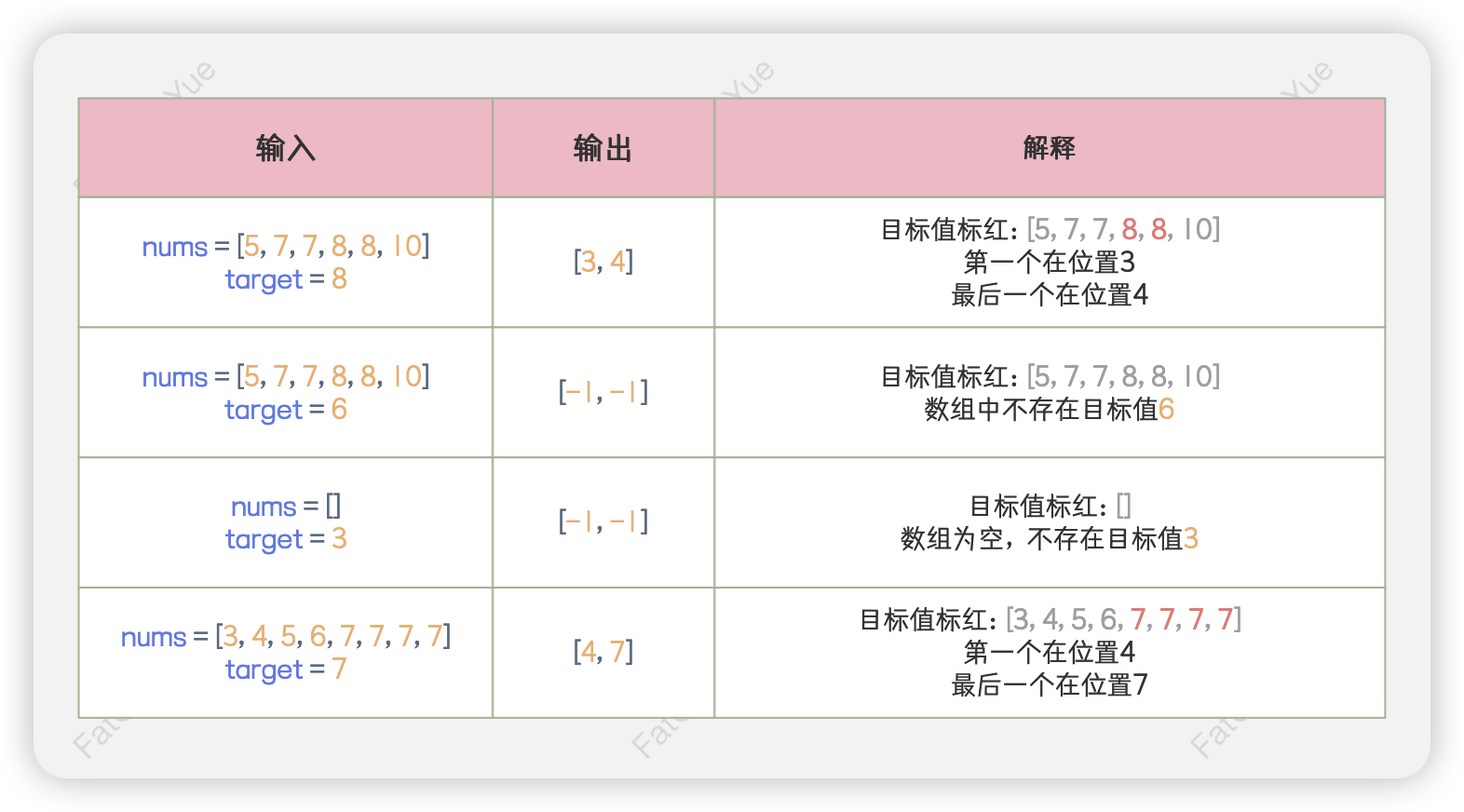
🖊️ 题解

​ 鉴于数组是升序排列且算法时间复杂度需为 $O(\log n)$ ，因此应当考虑二分查找来解决本题。

​ 通过二分查找，我们可以方便地找到数组中第一个大于或等于 $target$ 的元素的位置。那么如何寻找 $target$ 的最后一个位置呢？同样地，我们可以先找到第一个大于或等于 $target+1$ 的元素的位置，然后将其减去 $1$ 即可得到 $target$ 的最后一个位置。因此，我们需要一个二分查找方法来获取数组中第一个大于或等于指定值的位置，若不存在，则返回 $nums.length$。

​ 需要注意的是，尽管数组 $nums$ 中可能存在第一个大于或等于 $target$ 的元素，但并不一定存在与 $target$ 相等的元素。因此，在第一次二分查找后，必须进行判断，若找不到，则直接返回 $[-1,-1]$。此外，数组 $nums$ 中有可能不存在大于或等于 $target+1$ 的元素，即数组的最后一个位置上的元素为 $target$。在这种情况下，第二次二分查找的结果将返回数组的长度，将其减去 $1$ 也能得到正确答案。

java

public class Solution {
    public int[] searchRange(int[] nums, int target) {
        int start = binarySearch(nums, target);
        if (start == nums.length || nums[start] != target) {
            return new int[]{-1, -1};
        }
        int end = binarySearch(nums, target + 1) - 1;
        return new int[]{start, end};
    }

    private int binarySearch(int[] nums, int target) {
        int low = 0, high = nums.length - 1;
        while (low <= high) {
            int mid = low + ((high - low) >> 1);
            if (nums[mid] >= target) {
                high = mid - 1;
            } else {
                low = mid + 1;
            }
        }
        return low;
    }
}

typescript

function searchRange(nums: number[], target: number): number[] {
    const binarySearch = (target: number): number => {
        let low = 0, high = nums.length - 1;
        while (low <= high) {
            const mid = low + Math.floor((high - low) / 2);
            if (nums[mid] >= target) {
                high = mid - 1;
            } else {
                low = mid + 1;
            }
        }
        return low;
    }
    const start = binarySearch(target);
    if (start == nums.length || nums[start] != target) {
        return [-1, -1];
    }
    const end = binarySearch(target + 1) - 1;
    return [start, end];
}

💭 复杂度分析

​ 基于二分查找的解决方案的复杂度分析如下。

• 时间复杂度：$O(\log n)$。
• 空间复杂度：$O(1)$ 。