🤖 不同路径
📝 题目描述
一个机器人位于一个m x n网格的左上角(起点在下图中标记为Start)。机器人每次只能向下或者向右移动一步。机器人试图到达网格的右下角(终点在下图中标记为Finish)。
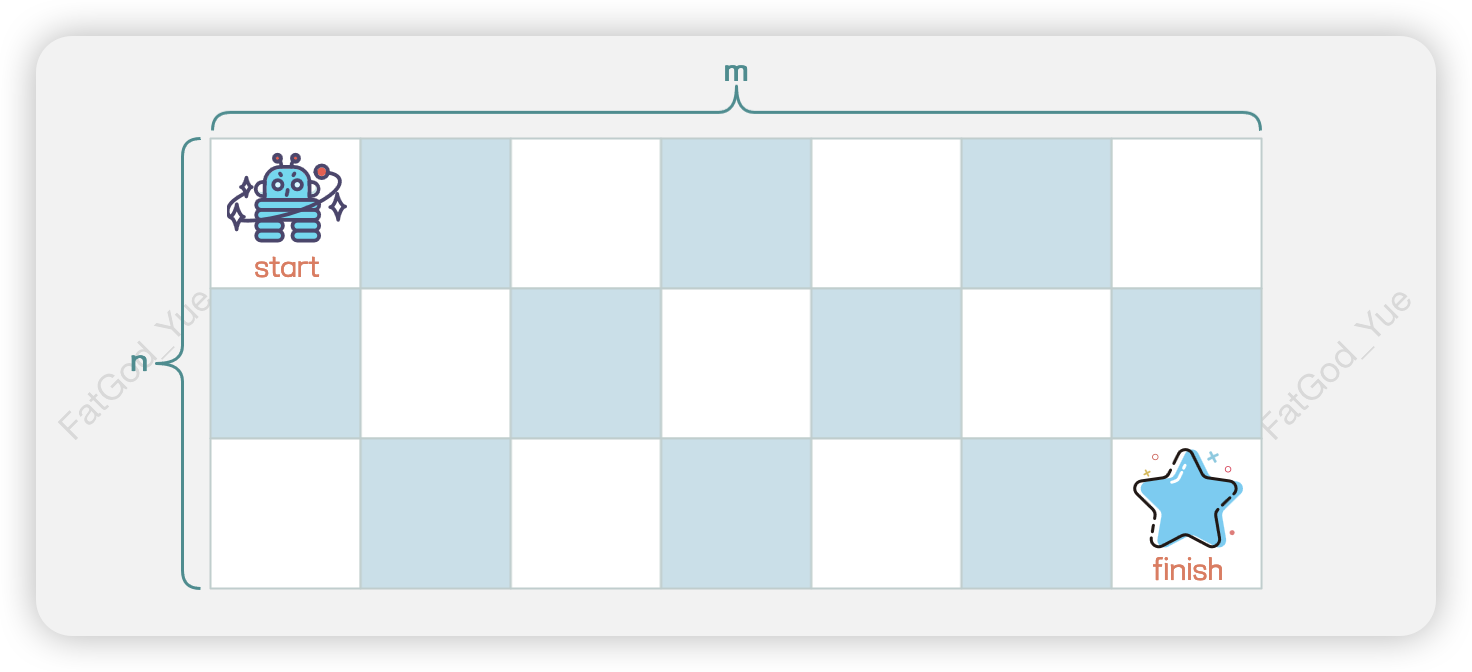
请你计算出机器人从起点到达终点共有多少条不同的路径。需要说明的是,1 x 1的网格的起点至终点的路径数取值为1。
📋 代码模版
class Solution {
public int uniquePaths(int m, int n) {
}
}function uniquePaths(m: number, n: number): number {
}💡 提示
🚀 示例
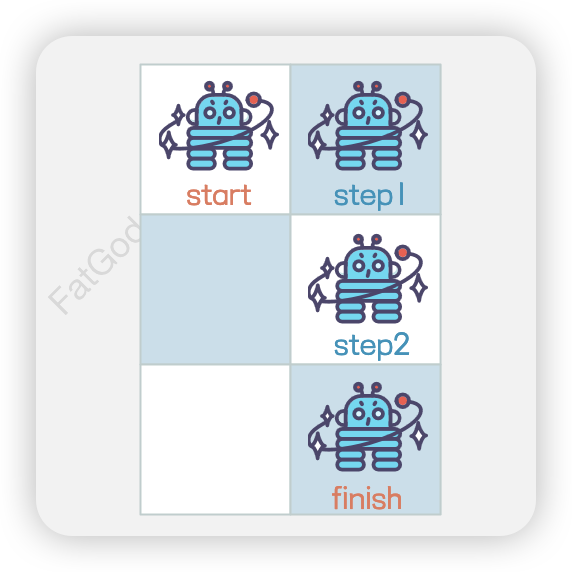
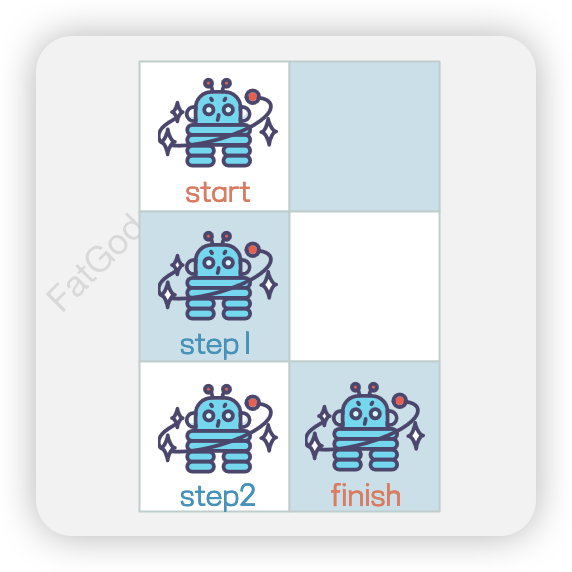
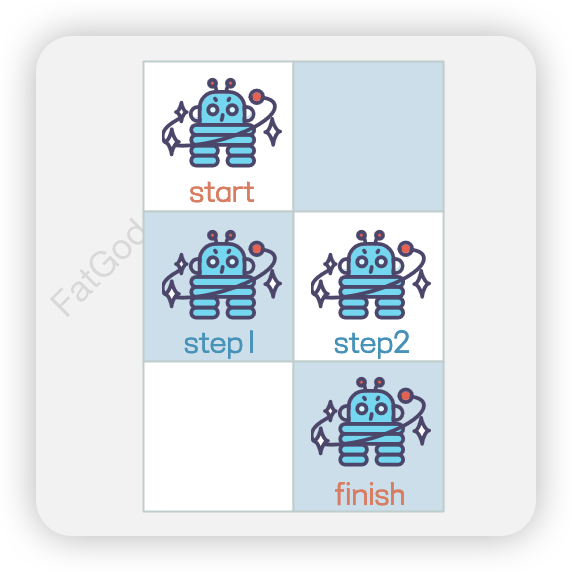
3 x 2
在3 x 2的网格上,机器人从起点到达终点的路径共有3条。
- 向右 → 向下 → 向下
- 向下 → 向下 → 向右
- 向下 → 向右 → 向下
2 x 5
在2 x 5的网格上,机器人从起点到达终点的路径共有5条。
- 向右 → 向右 → 向右 → 向右 → 向下
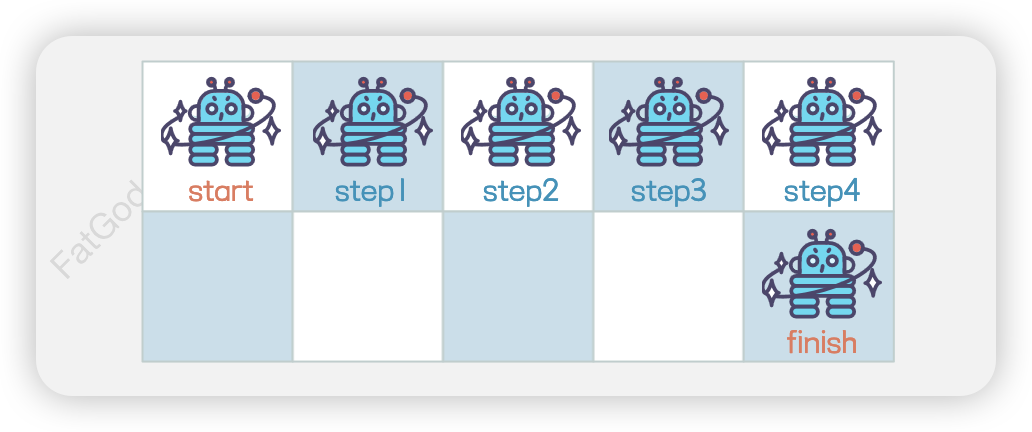
- 向下 → 向右 → 向右 → 向右 → 向右
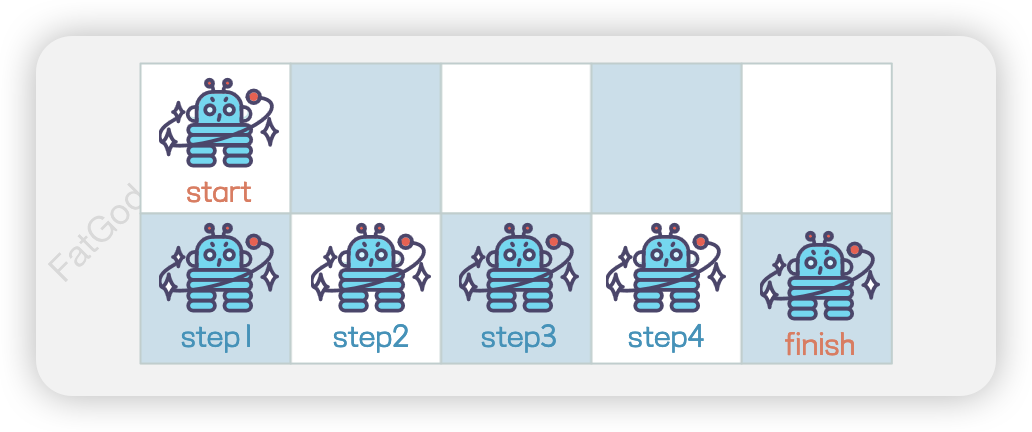
- 向右 → 向下 → 向右 → 向右 → 向右
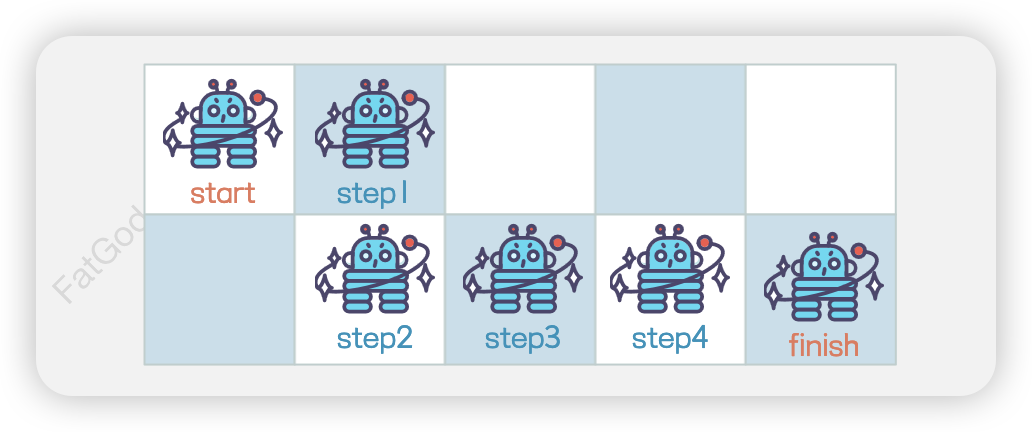
- 向右 → 向右 → 向下 → 向右 → 向右
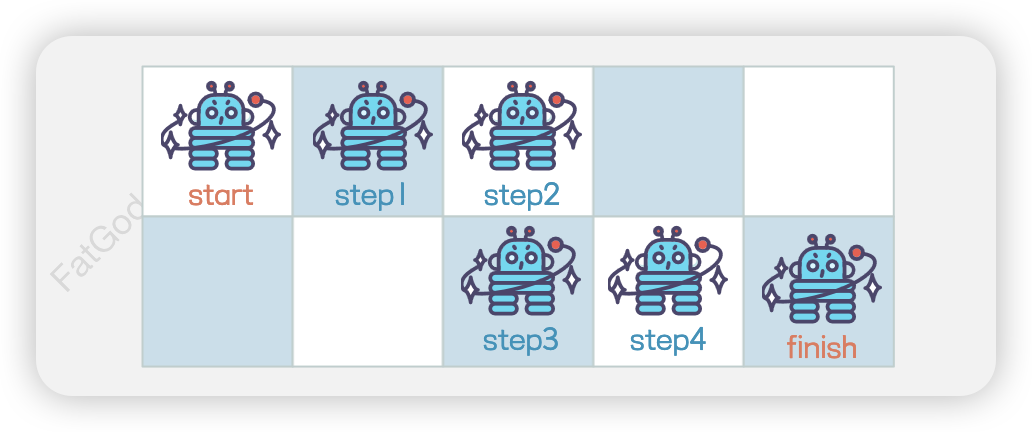
- 向右 → 向右 → 向右 → 向下 → 向右
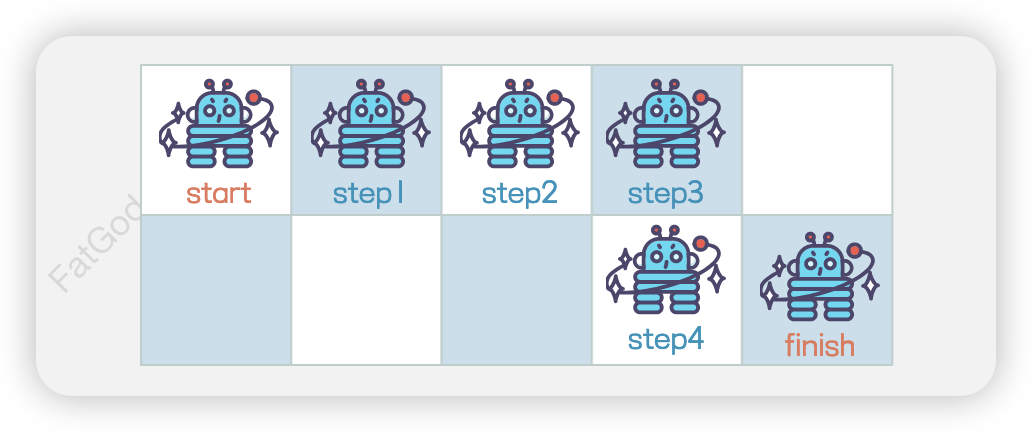
🖊️ 题解
记忆化搜索
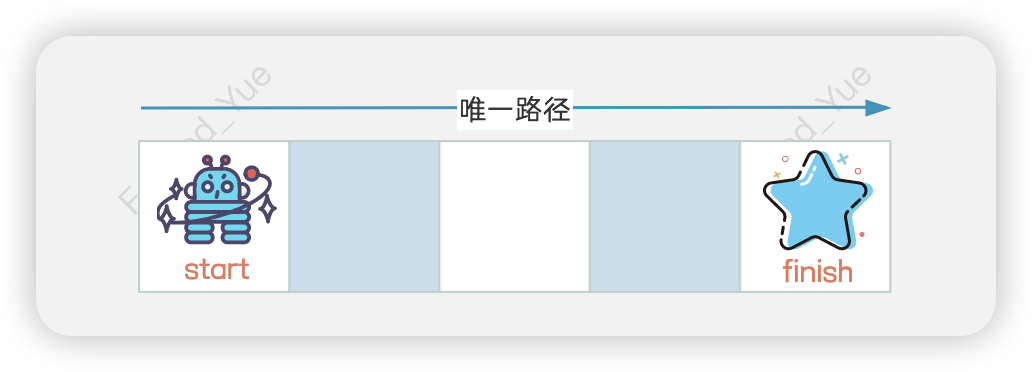
我们可以先考虑最简单的情况。如果网格只有一行(m = 1),由于机器人只能向右不能向左,因此对于这一行中的每个格子(包括终点),都只有一条路径。
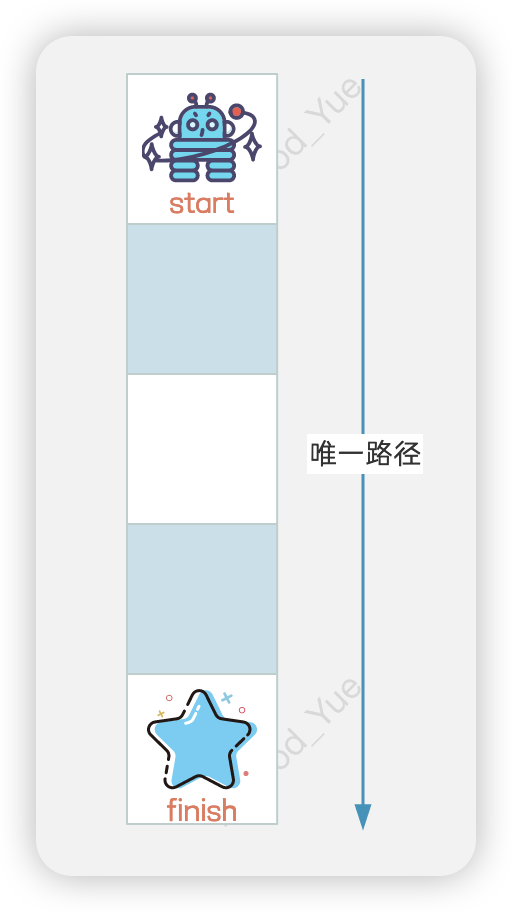
如果网格只有一列(n = 1),由于机器人只能向下不能向上,因此对于这一行中的每个格子(包括终点),也都只有一条路径。
如果网格(行列下标从1开始)有多行多列(n > 1 && m > 1),那机器人到达终点(m,n)的路径总数计算可以分为以下两种情况。
- 机器人到达格子
(m-1,n)共有多少条路径? - 机器人到达格子
(m,n-1)共有多少条路径?
而机器人到达终点(m,n)的路径总数就等于其到达格子(m-1,n)的路径总数加上其到达格子(m,n-1)的路径总数。因为如果想要到达格子(m,n),无非就是在格子(m-1,n)往下走一步,或在格子(m,n-1)往右走一步。
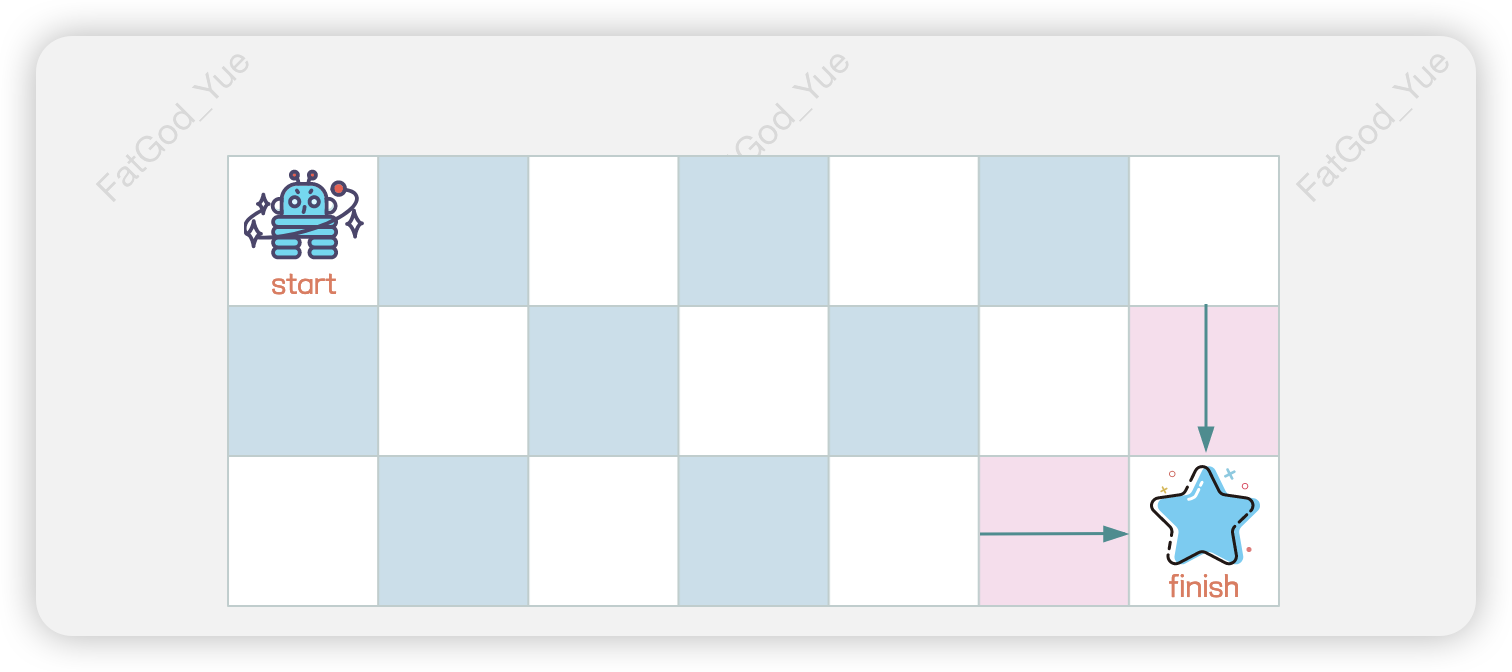
在上述过程中,原问题被拆分为两个子问题。通过仔细观察这两个子问题,我们发现它们与原问题相似,只是规模更小,并且当子问题的答案不明确时,我们仍然可以将其进一步分解为更小的子问题。
因此,该题可以使用深度优先搜索dfs来解决。我们定义
综上所述,我们很容易写出以下代码。
class Solution {
public int uniquePaths(int m, int n) {
if (m == 1 || n == 1) {
return 1;
}
return uniquePaths(m - 1, n) + uniquePaths(m, n - 1);
}
}function uniquePaths(m: number, n: number): number {
if (m == 1 || n == 1) {
return 1;
}
return uniquePaths(m - 1, n) + uniquePaths(m, n - 1);
} 😭但经过实践,当输入的m与n增大到一定阈值时,以上代码的提交大概率会因为超时而无法通过。
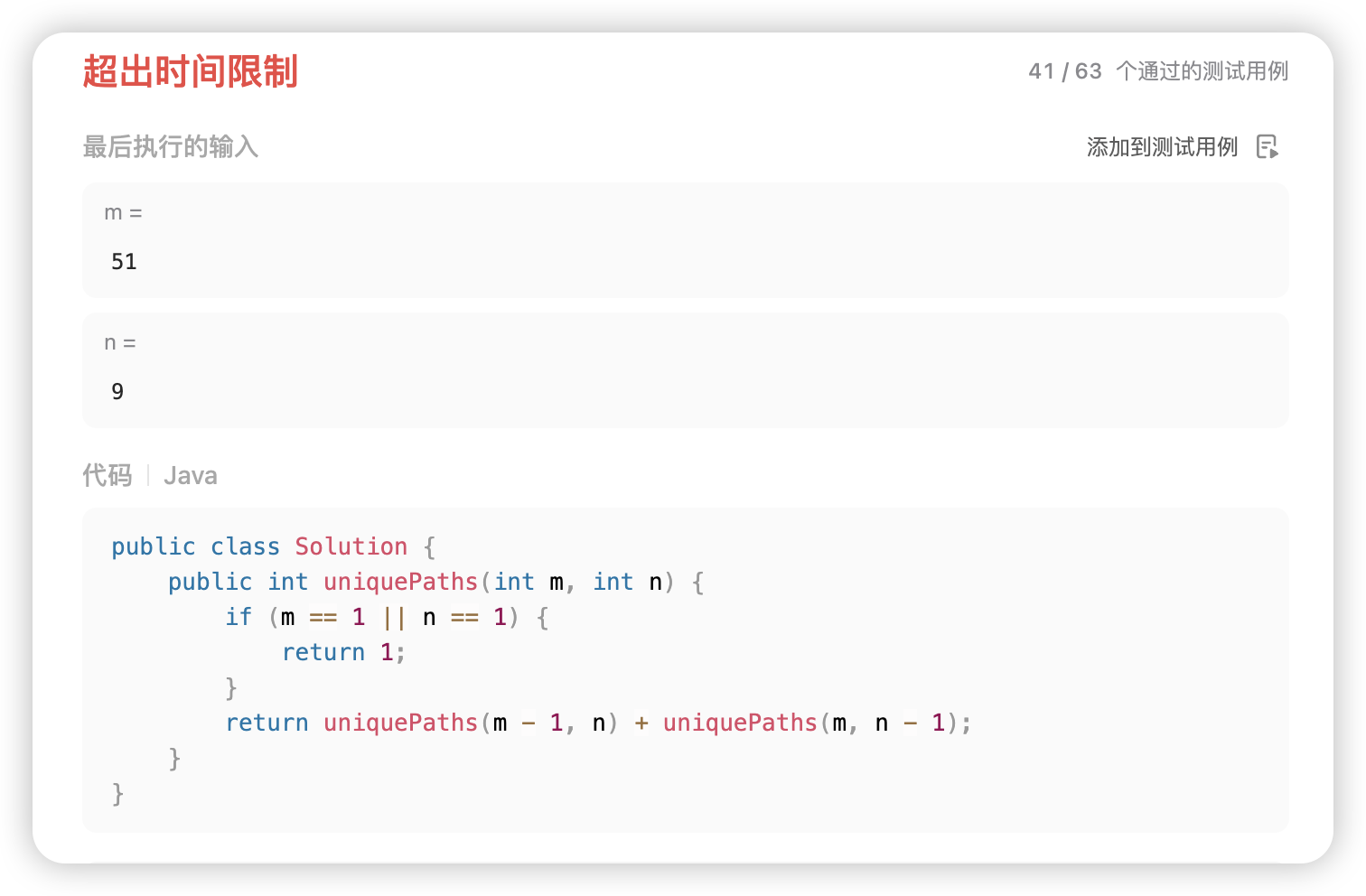
那么,导致以上代码运行效率低下的原因是什么呢?答案是多路递归带来的重复计算问题,在递归过程中,同一个格子的路径总数可能会被计算多次。为了解决这个问题,我们可以使用记忆化搜索方法,代码如下。
class Solution {
public int uniquePaths(int m, int n) {
int[][] memory = new int[m + 1][n + 1];
return dfs(m, n, memory);
}
private int dfs(int i, int j, int[][] memory) {
if (i == 1 || j == 1) {
return 1;
}
if (memory[i][j] != 0) {
return memory[i][j];
}
return memory[i][j] = dfs(i - 1, j, memory) + dfs(i, j - 1, memory);
}
}function uniquePaths(m: number, n: number): number {
const memory: number[][] = Array.from({ length: m + 1 },
() => Array(n + 1).fill(0));
const dfs = (i: number, j: number): number => {
if (i == 1 || j == 1) {
return 1;
}
if (memory[i][j] != 0) {
return memory[i][j];
}
return memory[i][j] = dfs(i - 1, j) + dfs(i, j - 1);
}
return dfs(m, n);
}动态规划
根据以上dfs的解法,我们可以很轻松地将其翻译成动态规划dp解法,具体步骤如下。
- 状态定义:设
为二维数组(逻辑上行列都从索引 1开始),其中代表⭐️机器人到达格子 的路径总数⭐️, 。 - 初始状态:根据边界条件,初始化
数组第一行与第一列,即 。 - 状态转移方程:
,其中 。 - 返回值:
,即到达终点网格 (m,n)的路径总数。
class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
dp[i][1] = 1;
}
for (int i = 1; i <= n; i++) {
dp[1][i] = 1;
}
for (int i = 2; i <= m; i++) {
for (int j = 2; j <= n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m][n];
}
}function uniquePaths(m: number, n: number): number {
const dp: number[][] = Array.from({ length: m + 1 },
() => Array(n + 1).fill(0));
for (let i = 1; i <= m; i++) {
dp[i][1] = 1;
}
for (let i = 1; i <= n; i++) {
dp[1][i] = 1;
}
for (let i = 2; i <= m; i++) {
for (let j = 2; j <= n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m][n];
} 以上算法需要一个很长的二维DP table(
这种技巧通常也被称为状态压缩,对应本题的算法代码如下。
class Solution {
public int uniquePaths(int m, int n) {
int[] cur = new int[n + 1];
for (int i = 1; i <= n; i++) {
cur[i] = 1;
}
for (int i = 2; i <= m; i++) {
for (int j = 2; j <= n; j++) {
cur[j] += cur[j - 1];
}
}
return cur[n];
}
}function uniquePaths(m: number, n: number): number {
const cur: number[] = Array(n + 1).fill(1);
for (let i = 2; i <= m; i++) {
for (let i = 2; i <= n; i++) {
cur[i] += cur[i - 1];
}
}
return cur[n];
}💭 复杂度分析
基于记忆化搜索的解决方案的复杂度分析如下。
- 时间复杂度:
。 - 空间复杂度:
。
基于动态规划的最优(状态压缩)解决方案的复杂度分析如下。
- 时间复杂度:
。 - 空间复杂度:
。

