🔗 第N个泰波那契数

📝 题目描述

​ 泰波那契序列$T_n$定义如下：

1. $T_0=0,T_1=1,T_2=1$
2. $T_{n+3}=T_n+T_{n+1}+T_{n+2}$，其中$n>=0$​

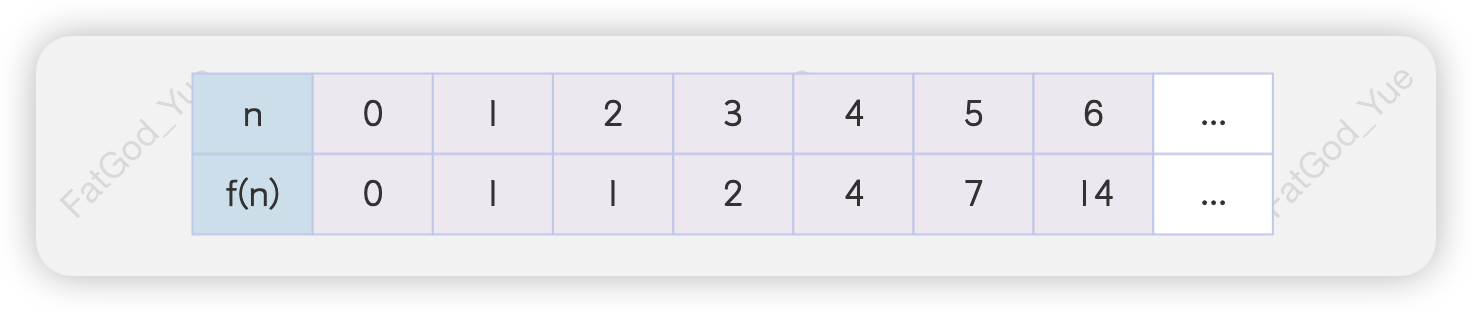
​ 现给你一个整数n，请返回第n个泰波那契数$T_n$的值。

📋 代码模版

java

class Solution {
    public int tribonacci(int n) {

    }
}

typescript

function tribonacci(n: number): number {

}

💡 提示

1. $0\le n\le 37$
2. 答案保证是一个32位整数，即$answer\le 2^{31}-1$

🚀 示例

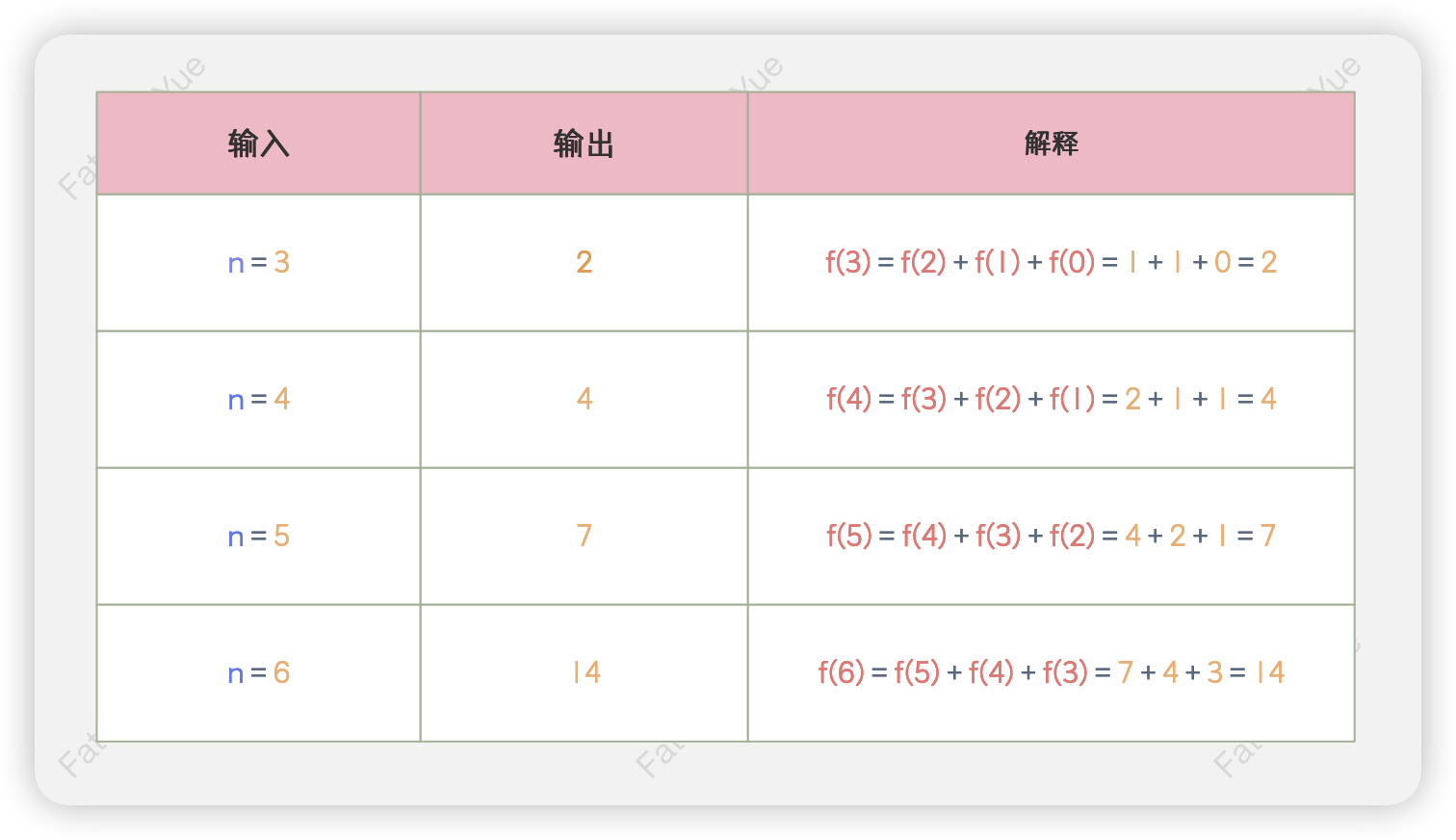
🖊️ 题解

​ 在解决这道题之前，建议先处理题目斐波那契数。

​ 斐波那契数列的特点是前两个数字固定，后续每个数字都等于前两个数字的和。而本题中的泰波那契序列与之类似，特点是前三个数字固定，之后每个数字都等于前三个数字的和。因此，本题的解决方法几乎与题斐波那契数一致。

记忆化搜索

​ 根据题目描述，本题的记忆化dfs的递归公式为$dfs(i)=dfs(i-1)+dfs(i-2)+dfs(i-3)$，递归边界为$dfs(0)=1,dfs(1)=1,dfs(2)=1$。其中，$dfs(i)$表示⭐️泰波那契序列中第i（2 < i <= n）个数字的值⭐️。

java

class Solution {
    public int tribonacci(int n) {
        int[] memory = new int[n + 1];
        return dfs(n, memory);
    }

    private int dfs(int i, int[] memory) {
        if (i <= 1) {
            return i;
        }
        if (i == 2) {
            return 1;
        }
        if (memory[i] != 0) {
            return memory[i];
        }
        return memory[i] = dfs(i - 1, memory) + dfs(i - 2, memory) + dfs(i - 3, memory);
    }
}

typescript

function tribonacci(n: number): number {
    const memory: number[] = [];
    const dfs = (i: number): number => {
        if (i <= 1) {
            return i;
        }
        if (i == 2) {
            return 1;
        }
        if (memory[i]) {
            return memory[i];
        }
        return memory[i] = dfs(i - 1) + dfs(i - 2) + dfs(i - 3);
    }
    return dfs(n);
}

动态规划

​ 根据以上dfs的解法，我们可以很轻松地将其翻译成动态规划dp解法，具体步骤如下。

1. 状态定义：设 $dp$ 为一维数组，其中 $dp[i]$ 代表⭐️泰波那契序列中第i个数字的值⭐️。
2. 初始状态：根据边界条件，初始化 $dp$ 数组的前三项，即$dp[0] = 0, dp[1] = 1, dp[2] = 1 $。
3. 状态转移方程：$dp[i]=dp[i-1]+dp[i-2]+dp[i-3]$，其中 $3\le i\le n$。
4. 返回值：$dp[n]$，即$T_n$​的值。

java

class Solution {
    public int tribonacci(int n) {
        if (n <= 1) {
            return n;
        }
        int[] dp = new int[n + 1];
        dp[0] = 0;
        dp[1] = 1;
        dp[2] = 1;
        for (int i = 3; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];
        }
        return dp[n];
    }
}

typescript

function tribonacci(n: number): number {
    if (n <= 1) {
        return n;
    }
    const dp: number[] = [];
    dp[0] = 0;
    dp[1] = 1;
    dp[2] = 1;
    for (let i = 3; i <= n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];
    }
    return dp[n];
}

​ 为了减小dp算法的空间复杂度，我们可以采用状态压缩技巧，即用若干变量替代 $dp$​ 数组存储状态。

java

class Solution {
    public int tribonacci(int n) {
        if (n <= 1) {
            return n;
        }
        int pre1 = 0, pre2 = 1, cur = 1;
        for (int i = 3; i <= n; i++) {
            int sum = pre1 + pre2 + cur;
            pre1 = pre2;
            pre2 = cur;
            cur = sum;
        }
        return cur;
    }
}

typescript

function tribonacci(n: number): number {
    if (n <= 1) {
        return n;
    }
    let pre1 = 0, pre2 = 1, cur = 1;
    for (let i = 3; i <= n; i++) {
        const sum = pre1 + pre2 + cur;
        pre1 = pre2;
        pre2 = cur;
        cur = sum;
    }
    return cur;
}

💭 复杂度分析

​ 基于记忆化搜索的解决方案的复杂度分析如下。

• 时间复杂度：$O(n)$。
• 空间复杂度：$O(n)$ 。

​ 基于动态规划的最优（状态压缩）解决方案的复杂度分析如下。

• 时间复杂度：$O(n)$。
• 空间复杂度：$O(1)$ 。