🔽 下一个更大元素 I

📝 题目描述

​ 给定两个没有重复元素的数组nums1和nums2，下标从0开始计数，其中nums1是nums2的子集。nums1中的数字x的下一个更大元素是指：数字x在nums2中对应位置右侧的第一个比x大的元素。

​ 对于每个0 <= i < nums1.length，找出满足nums1[i] == nums2[j]条件的下标j，并且在nums2中确定nums2[j]的下一个更大元素，如果不存在下一个更大元素，那么本次查询的答案为-1。

​ 请你返回一个长度为nums1.length的数组ans作为返回值，并满足ans[i]是nums1[i]的下一个更大元素。

📋 代码模版

class Solution {
    public int[] nextGreaterElement(int[] nums1, int[] nums2) {

    }
}

💡 提示

1. $1<=nums1.length<=nums2.length<=1000$
2. $0<=nums1[i]<={10}^4$
3. $0<=nums2[i]<={10}^4$
4. $nums1$ 和 $nums2$​ 中所有整数互不相同
5. $nums1$ 中出现的所有整数同样出现在 $nums2$

🚀 示例

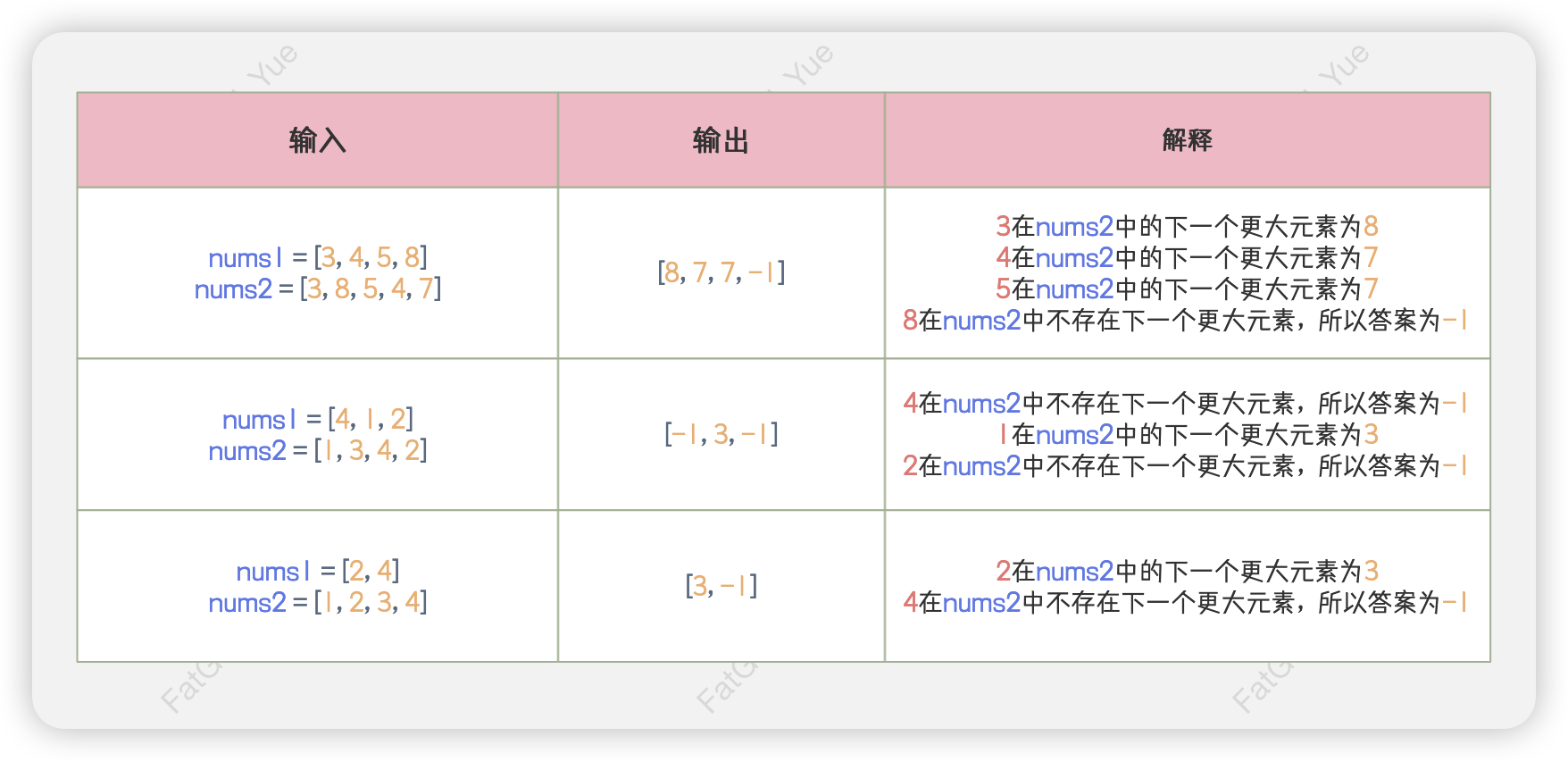
🖊️ 题解

模拟

​ 一个最简单的解题做法就是根据题意对整个过程进行模拟：遍历nums1数组，在每一轮遍历中，需先找到nums1[i]值在nums2中的位置（下标）j，然后再从下标j开始，在nums2中往后找到第一个比nums2[j]大的元素，如果能找到，则将查询结果作为ans[i]的值，如果未能找到，则查询结果为-1。

class Solution {
    public int[] nextGreaterElement(int[] nums1, int[] nums2) {
        int[] ans = new int[nums1.length];
        int n = nums1.length, m = nums2.length;
        for (int i = 0; i < n; i++) {
            int j = 0;
            while (j < m && nums2[j] != nums1[i]) {
                j++;
            }
            int k = j + 1;
            while (k < m && nums2[k] <= nums2[j]) {
                k++;
            }
            ans[i] = k < m ? nums2[k] : -1;
        }
        return ans;
    }
}

单调栈

​ 对于nums2数组中的每个元素，它的下一个更大元素查询只关心其后续的元素，因此我们可以采用反向遍历。这样一来，当我们处理nums2[i]元素时，它后续的元素就已经被处理过了。

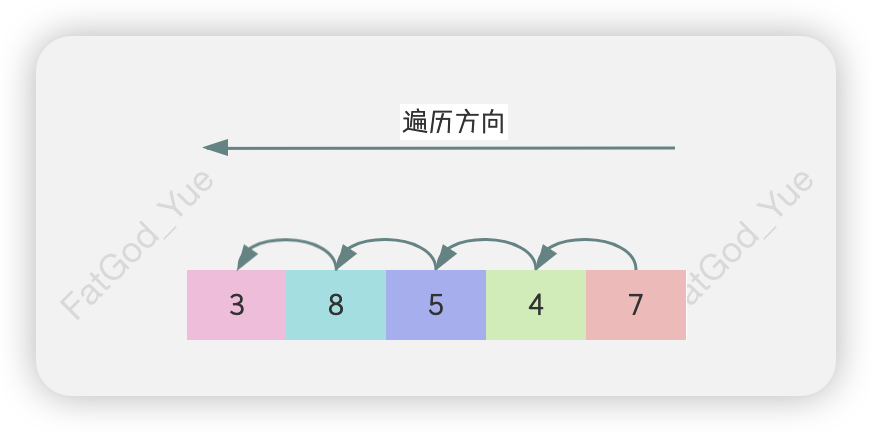
​ 因此，该题解法的关键在于：在反向遍历过程中，应维护一种什么样的数据结构，能够更高效地计算nums2中每个元素右边第一个更大的值。答案是单调栈，每一轮遍历中，维护一个从栈底到栈顶单调递减的单调栈，具体步骤如下。

1. 创建一个初始为空的辅助栈。
2. 反向遍历nums2数组。在每一轮遍历中，需沿栈顶至栈底方向，在栈中找到第一个大于当前元素nums2[i]的元素，并将其作为nums2[i]的下一个更大元素，同时将nums2[i]压入栈中。在查询过程中，若栈顶元素不符合条件，则直接将其从栈中弹出，这是因为对于nums2[i]左边的元素来说，小于等于nums2[i]的右边元素不可能会是下一个更大元素。需要注意的是，在每次遍历过程中，可能会存在边界问题，即栈为空，此时则说明nums2[i]后没有大于它的元素，查询结果应为-1。

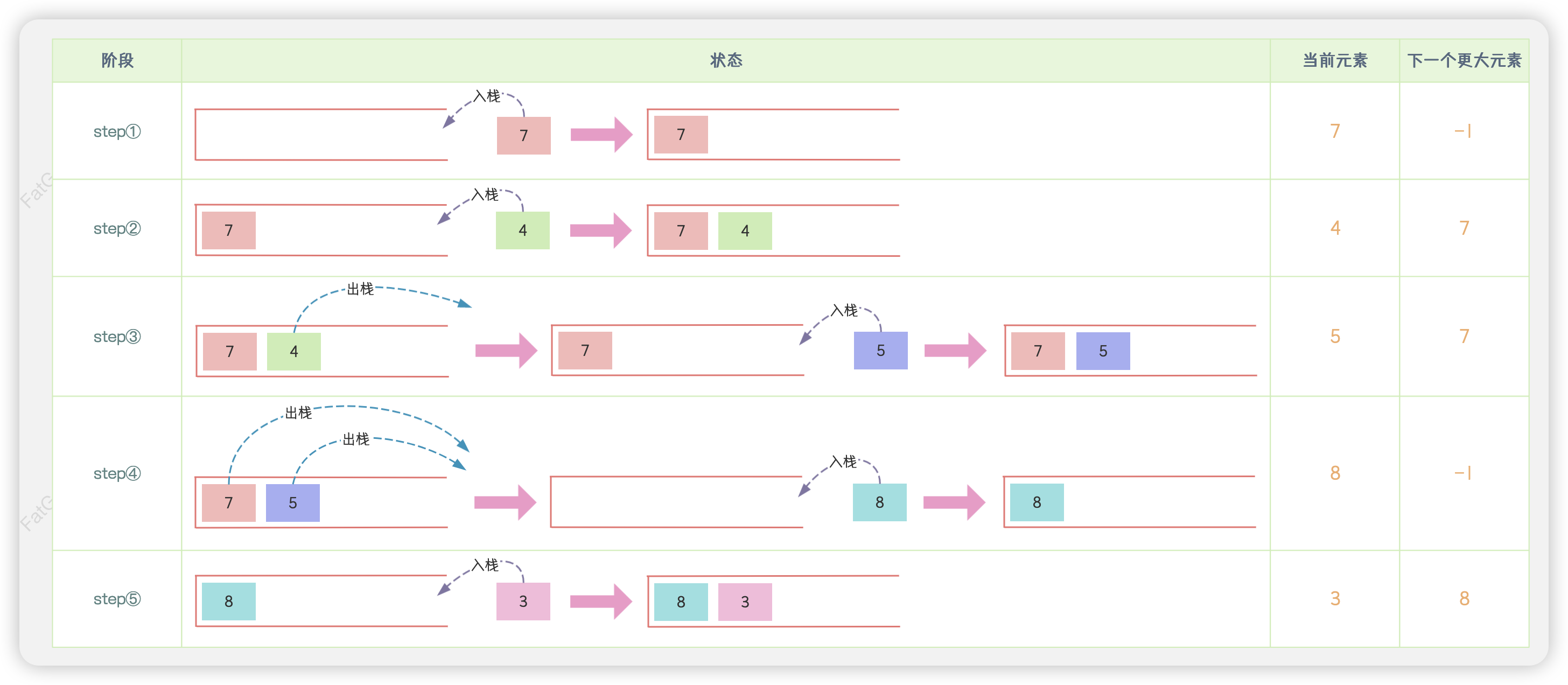
​ ⭐️经过以上步骤，我们就能得到nums2中每一个元素的下一个更大元素。又由于nums1是nums2的子集，nums1的每一个元素的下一个更大元素也能够确定。为了提高查询效率，我们可以提前创建一个哈希表，并在反向遍历nums2数组的每一轮中，建立nums2[i]与nums2[i]的下一个更大元素之间的映射关系。这样一来，当我们获取nums1中元素的下一个更大元素的时间复杂度就为$O(1)$。

class Solution {
    public int[] nextGreaterElement(int[] nums1, int[] nums2) {
        Deque<Integer> monotonicStack = new ArrayDeque<>();
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = nums2.length - 1; i >= 0; i--) {
            while (!monotonicStack.isEmpty() && monotonicStack.peek() <= nums2[i]) {
                monotonicStack.pop();
            }
            map.put(nums2[i], monotonicStack.isEmpty() ? -1 : monotonicStack.peek());
            monotonicStack.push(nums2[i]);
        }
        int[] ans = new int[nums1.length];
        for (int i = 0; i < nums1.length; i++) {
            ans[i] = map.get(nums1[i]);
        }
        return ans;
    }
}

💭 复杂度分析

​ 基于模拟的解决方案的复杂度分析如下。

• 时间复杂度：$O(n\ast m)$，其中$n$为nums1的长度，$m$为nums2的长度。
• 空间复杂度：$O(1)$ ，返回值不计入空间复杂度。

​ 基于单调栈的解决方案的复杂度分析如下。

• 时间复杂度：$O(m+n)$，其中$n$为nums1的长度，$m$为nums2的长度，$n+m$表示分别遍历两次。
• 空间复杂度：$O(m)$ 。