🧐 最小栈

📝 题目描述

​ 请你设计一个支持push、pop、top操作，并能在常数时间内检索到最小元素的栈。

​ 实现MinStack包含以下几部分内容。

1. MinStack(): 初始化栈对象。
2. void push(int val): 将元素val压入栈中。
3. void pop(): 弹出栈顶元素。
4. int top(): 获取栈顶元素。
5. int getMin(): 获取栈中的最小元素。

📋 代码模版

class MinStack {

    public MinStack() {

    }
    
    public void push(int val) {

    }
    
    public void pop() {

    }
    
    public int top() {

    }
    
    public int getMin() {

    }
}

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(val);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.getMin();
 */

💡 提示

1. ${-2}^{31}<=val<=2^{31}-1$
2. pop、top和getMin操作总是在非空栈上调用
3. push、pop、top和getMin最多被调用 $3\ast {10}^4$ 次

🚀 示例

输入

public static void main(String[] args) {
    MinStack minStack = new MinStack();
    minStack.push(2);
    minStack.push(4);
    minStack.push(3);
    minStack.push(7);
    minStack.push(1);
    minStack.push(1);
    minStack.push(5);
    int min1 = minStack.getMin();
    for (int i = 0; i < 2; i++) {
        minStack.pop();
    }
    int min2 = minStack.getMin();
    minStack.pop();
    int top = minStack.top();
    int min3 = minStack.getMin();
    System.out.println(min1);
    System.out.println(min2);
    System.out.println(top);
    System.out.println(min3);
}

输出

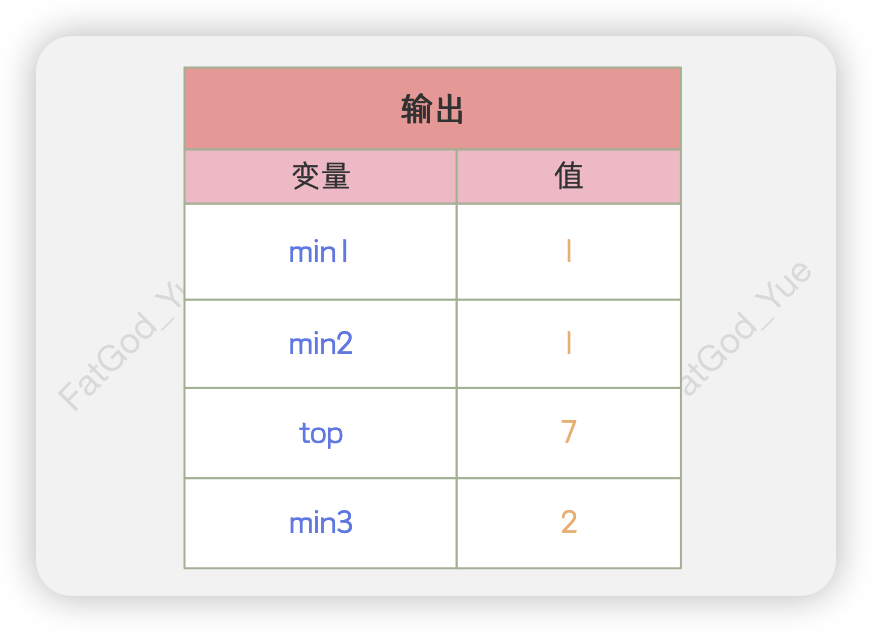
🖊️ 题解

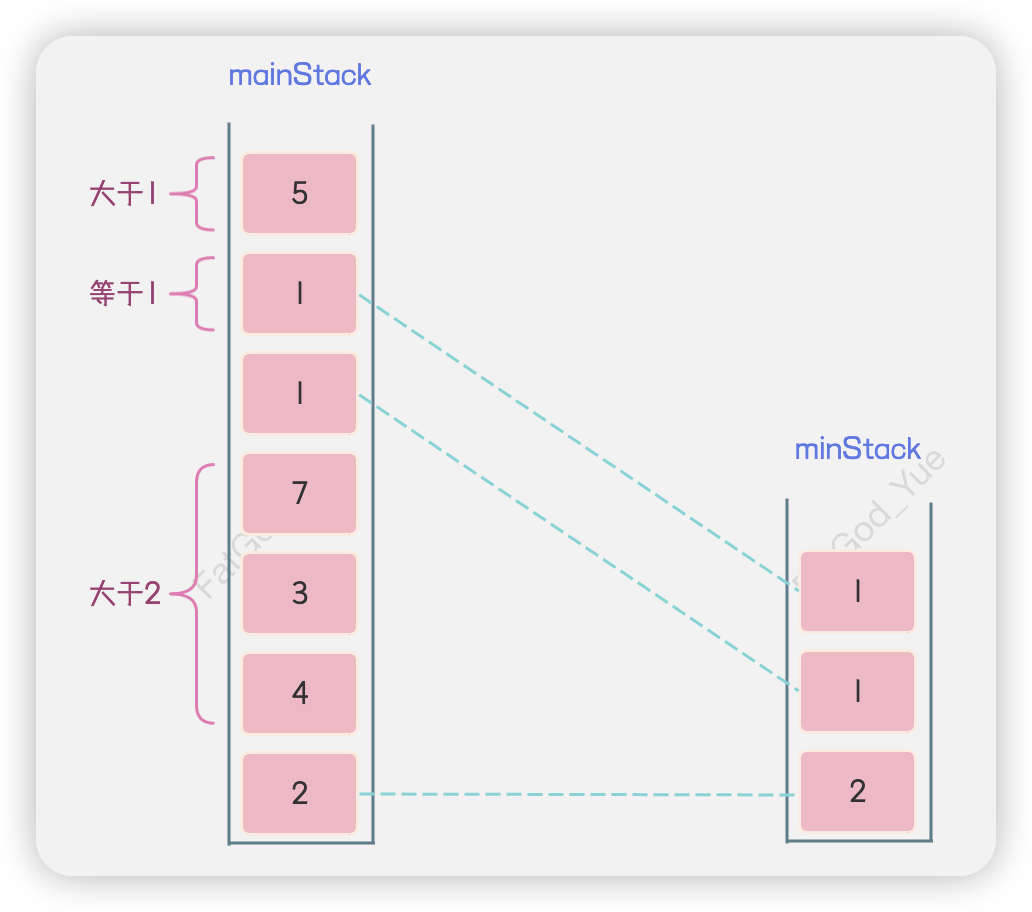
​ 由于栈先进后出的特点，所以对于栈中的每一个元素来说，如果其下方存在比它值还小的元素的话，那么栈中的最小元素就永远不可能为自身。例如，在以下示例中，当7、3或4存在栈中时，它们不可能是最小元素，因为它们底下还存在2这个元素。

​ 因此，我们可以利用辅助栈向上依次记录最小值来解决这个问题，具体步骤如下。

1. 创建一个辅助栈minStack。
2. 实现push方法：将新的val压入主栈mainStack中，若minStack大于等于val，则将val同时压入minStack中，使得val成为新的栈中最小值。此时，需要考虑minStack本身就为空的边界情况，在这种条件下，val也应成为新的最小值。
3. 实现pop方法：弹出主栈mainStack中的栈顶元素，若该元素的值与minStack栈顶元素的值相同，则表示该元素是栈中的最小值，此时应弹出minStack栈顶元素，这保证了minStack中的栈顶元素始终为mainStack中的最小值。
4. 实现getMin方法：返回minStack栈顶值即可。

---

​ 该解法其实是基于主栈，从栈底至栈顶维护一个向上单调递减的单调栈。

class MinStack {
    private final Deque<Integer> mainStack;
    private final Deque<Integer> minStack;

    public MinStack() {
        mainStack = new ArrayDeque<>();
        minStack = new ArrayDeque<>();
    }

    public void push(int val) {
        mainStack.push(val);
        if (minStack.isEmpty() || minStack.peek() >= val) {
            minStack.push(val);
        }
    }

    public void pop() {
        Integer pop = mainStack.pop();
        if (!minStack.isEmpty() && minStack.peek().equals(pop)) {
            minStack.pop();
        }
    }

    public int top() {
        return mainStack.peek();
    }

    public int getMin() {
        return minStack.peek();
    }
}

💭 复杂度分析

​ 基于辅助栈的解决方案的复杂度分析如下。

• 时间复杂度：push、pop、top和getMin操作皆为$O(1)$。
• 空间复杂度：$O(n)$。