🎨 边界着色

📝 题目描述

给你一个大小为m x n的整数矩阵grid，表示一个网格。另给你三个整数row、col和color。网格中的每个值表示该位置处的网格块的颜色。

如果两个方块在任意 $4$ 个方向上相邻，则称它们相邻。

如果两个方块具有相同的颜色且相邻，它们则属于同一个连通分量。

连通分量的边界是指连通分量中满足下述条件之一的所有网格块：

在上、下、左、右任意一个方向上与不属于同一连通分量的网格块相邻
在网格的边界上（第一行/列或最后一行/列）

请你使用指定颜色color为所有包含网格块grid[row][col]的连通分量的边界进行着色。并返回最终的网格grid。

📋 代码模板

javatypescript

java

class Solution {
    public int[][] colorBorder(int[][] grid, int row, int col, int color) {

    }
}

typescript

function colorBorder(grid: number[][], row: number, col: number, color: number): number[][] {
    
}

💡 提示

$m == g r i d . l e n g t h$
$n == g r i d [i] . l e n g t h$
$1 \leq m \leq 50$
$1 \leq m \leq 50$
$1 \leq g r i d [i] [j] \leq 1000$
$1 \leq c o l o r \leq 1000$
$0 \leq r o w < m$
$0 \leq c o l < n$

🚀 示例

示例一

输入grid为[[1,1],[1,2]]、row为0、col为0、color为3，输出为[[3,3],[3,2]]。连通分量的边界着色过程如下图所示。

示例一

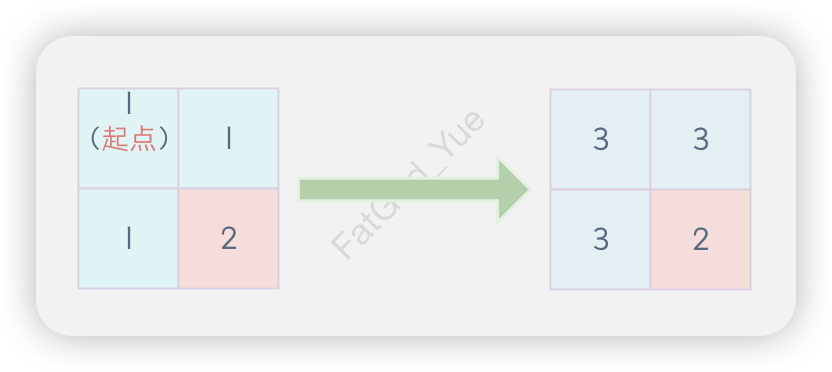
示例二

输入grid为[[1,2,2],[2,3,2]]、row为0、col为1、color为3，输出为[[1,3,3],[2,3,3]]。连通分量的边界着色过程如下图所示。

示例二

示例三

输入grid为[[1,1,1],[1,1,1],[1,1,1]]、row为1、col为1、color为2，输出为[[2,2,2],[2,1,2],[2,2,2]]。连通分量的边界着色过程如下图所示。

示例三

示例四

输入grid为[[0,8,8,8,2,2],[9,6,2,2,2,2],[9,6,2,2,2,2],[6,6,6,2,7,7]]、row为1、col为4、color为1，输出为[[0,8,8,8,1,1],[9,6,1,2,2,1],[9,6,1,2,1,1],[6,6,6,1,7,7]]。连通分量的边界着色过程如下图所示。

示例四

🖊️ 题解

本题要求从一个起始节点 $[r o w, c o l]$ 开始，对其所属的连通分量的边界进行着色，即将边界单元格的值填充为指定的 $c o l o r$ 值。而边界的判定标准为：单元格位于网格的边缘，或者与任何非 $g r i d [r o w] [c o l]$ 值的单元格相邻。

我们可以从起始节点 $[r o w, c o l]$ 开始行DFS或BFS。在搜索过程中，每遇到一个尚未访问过且值为 $g r i d [r o w] [c o l]$ 的单元格，则判断它是否为边界单元格，如果是边界单元格，那么将其标记为”应着色“状态，否则将其标记为”已访问“状态，”应着色“状态可以看成一种特殊的”已访问“状态。搜索结束后，扫描整个二维网格，将状态为”已访问“的单元格的值更新为原始值 $g r i d [r o w] [c o l]$ ，而将状态为”应着色“的单元格的值更新为 $c o l o r$ 。

为了进一步节省算法的空间，我们可以直接将网格中单元格的值更新为 $- 2$ ，表示其已经被访问。同样地，我们也可以直接将网格中单元格的值更新为 $- 1$ ，表示其应该被着色。

DFS

javatypescript

java

class Solution {
    private final static int[][] DIRS = new int[][]{{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
    private final static int STAINED = -1;
    private final static int VISITED = -2;

    public int[][] colorBorder(int[][] grid, int row, int col, int color) {
        int m = grid.length, n = grid[0].length, originalColor = grid[row][col];
        dfs(grid, row, col, originalColor);
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == VISITED) {
                    grid[i][j] = originalColor;
                    continue;
                }
                if (grid[i][j] == STAINED) {
                    grid[i][j] = color;
                }
            }
        }
        return grid;
    }

    private void dfs(int[][] grid, int i, int j, int originalColor) {
        if (i < 0 || i > grid.length - 1 || j < 0 || j > grid[0].length - 1
                || grid[i][j] != originalColor) {
            return;
        }
        boolean isBorder = isBorder(grid, i, j);
        grid[i][j] = isBorder ? STAINED : VISITED;
        for (int d = 0; d < 4; d++) {
            dfs(grid, i + DIRS[d][0], j + DIRS[d][1], originalColor);
        }
    }

    private boolean isBorder(int[][] grid, int i, int j) {
        int m = grid.length, n = grid[0].length;
        boolean isBorder = i == 0 || i == m - 1 || j == 0 || j == n - 1;
        for (int d = 0; d < 4 && !isBorder; d++) {
            int nextI = i + DIRS[d][0], nextJ = j + DIRS[d][1];
            int nextVal = grid[nextI][nextJ];
            isBorder = nextVal != grid[i][j] && nextVal != STAINED && nextVal != VISITED;
        }
        return isBorder;
    }
}

typescript

const DIRS: number[][] = [[-1, 0], [1, 0], [0, -1], [0, 1]];
const STAINED = -1, VISITED = -2;

function colorBorder(grid: number[][], row: number, col: number, color: number): number[][] {
    const m = grid.length, n = grid[0].length, originalColor = grid[row][col];
    const isBorder = (i: number, j: number): boolean => {
        let isBorder: boolean = i == 0 || i == m - 1 || j == 0 || j == n - 1;
        for (let d = 0; d < 4 && !isBorder; d++) {
            const nextI = i + DIRS[d][0], nextJ = j + DIRS[d][1], nextVal = grid[nextI][nextJ];
            isBorder = nextVal != grid[i][j] && nextVal != STAINED && nextVal != VISITED;
        }
        return isBorder;
    }
    const dfs = (i: number, j: number): void => {
        if (i < 0 || i > m - 1 || j < 0 || j > n - 1 || grid[i][j] != originalColor) {
            return;
        }
        grid[i][j] = isBorder(i, j) ? STAINED : VISITED;
        for (let d = 0; d < 4; d++) {
            dfs(i + DIRS[d][0], j + DIRS[d][1]);
        }
    }
    dfs(row, col);
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            if (grid[i][j] == VISITED) {
                grid[i][j] = originalColor;
                continue;
            }
            if (grid[i][j] == STAINED) {
                grid[i][j] = color;
            }
        }
    }
    return grid;
}

BFS

javatypescript

java

class Solution {
    private final static int[][] DIRS = new int[][]{{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
    private final static int STAINED = -1;
    private final static int VISITED = -2;

    public int[][] colorBorder(int[][] grid, int row, int col, int color) {
        int m = grid.length, n = grid[0].length, originalColor = grid[row][col];
        Queue<int[]> queue = new LinkedList<>();
        queue.offer(new int[]{row, col});
        grid[row][col] = isBorder(grid, row, col) ? STAINED : VISITED;
        while (!queue.isEmpty()) {
            int[] cell = queue.poll();
            int oldI = cell[0], oldJ = cell[1];
            for (int d = 0; d < 4; d++) {
                int i = oldI + DIRS[d][0], j = oldJ + DIRS[d][1];
                if (i >= 0 && i < m && j >= 0 && j < n && grid[i][j] == originalColor) {
                    queue.offer(new int[]{i, j});
                    grid[i][j] = isBorder(grid, i, j) ? STAINED : VISITED;
                }
            }
        }
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == VISITED) {
                    grid[i][j] = originalColor;
                    continue;
                }
                if (grid[i][j] == STAINED) {
                    grid[i][j] = color;
                }
            }
        }
        return grid;
    }

    private boolean isBorder(int[][] grid, int i, int j) {
        int m = grid.length, n = grid[0].length;
        boolean isBorder = i == 0 || i == m - 1 || j == 0 || j == n - 1;
        for (int d = 0; d < 4 && !isBorder; d++) {
            int nextI = i + DIRS[d][0], nextJ = j + DIRS[d][1];
            int nextVal = grid[nextI][nextJ];
            isBorder = nextVal != grid[i][j] && nextVal != STAINED && nextVal != VISITED;
        }
        return isBorder;
    }
}

typescript

const DIRS: number[][] = [[-1, 0], [1, 0], [0, -1], [0, 1]];
const STAINED = -1, VISITED = -2;

function colorBorder(grid: number[][], row: number, col: number, color: number): number[][] {
    const m = grid.length, n = grid[0].length, originalColor = grid[row][col];
    const isBorder = (i: number, j: number): boolean => {
        let isBorder: boolean = i == 0 || i == m - 1 || j == 0 || j == n - 1;
        for (let d = 0; d < 4 && !isBorder; d++) {
            const nextI = i + DIRS[d][0], nextJ = j + DIRS[d][1], nextVal = grid[nextI][nextJ];
            isBorder = nextVal != grid[i][j] && nextVal != STAINED && nextVal != VISITED;
        }
        return isBorder;
    }
    const queue: number[][] = [];
    queue.push([row, col]);
    grid[row][col] = isBorder(row, col) ? STAINED : VISITED;
    while (queue.length > 0) {
        const cell: number[] = queue.shift()!;
        const oldI = cell[0], oldJ = cell[1];
        for (let d = 0; d < 4; d++) {
            const i = oldI + DIRS[d][0], j = oldJ + DIRS[d][1];
            if (i >= 0 && i < m && j >= 0 && j < n && grid[i][j] == originalColor) {
                queue.push([i, j]);
                grid[i][j] = isBorder(i, j) ? STAINED : VISITED;
            }
        }
    }
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            if (grid[i][j] == VISITED) {
                grid[i][j] = originalColor;
                continue;
            }
            if (grid[i][j] == STAINED) {
                grid[i][j] = color;
            }
        }
    }
    return grid;
}

💭 复杂度分析

基于DFS的解决方案的复杂度分析如下。

时间复杂度： $O (m n)$ 。其中 $m$ 与 $n$ 分别为网格的行数和列数。
空间复杂度： $O (m n)$ 。在最坏情况下，整个网格均为陆地，深度优先搜索的深度达到 $m n$ 。

基于BFS的解决方案的复杂度分析如下。

时间复杂度： $O (m n)$ 。其中 $m$ 与 $n$ 分别为网格的行数和列数。
空间复杂度： $O (m n)$ 。

🎨 边界着色 ​

📝 题目描述 ​

📋 代码模板 ​

💡 提示 ​

🚀 示例 ​

示例一 ​

示例二 ​

示例三 ​

示例四 ​

🖊️ 题解 ​

DFS ​

BFS ​

💭 复杂度分析 ​

🎨 边界着色

📝 题目描述

📋 代码模板

💡 提示

🚀 示例

示例一

示例二

示例三

示例四

🖊️ 题解

DFS

BFS

💭 复杂度分析