🔽 下一个更大元素 II

📝 题目描述

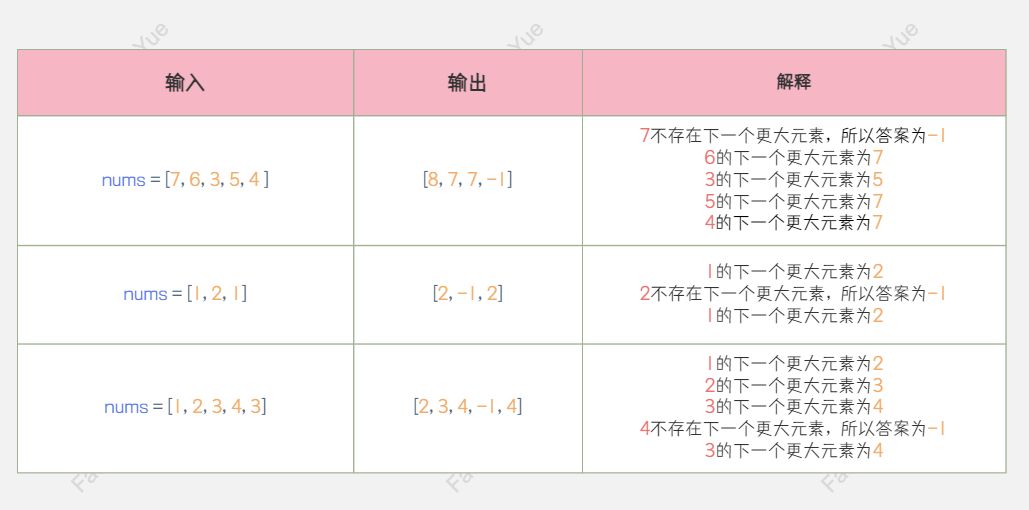
​ 给定一个循环数组nums（nums[nums.length - 1]的下一个元素是nums[0]），请返回nums中每个元素的下一个更大元素。

​ 数字x的下一个更大元素是指：数组循环遍历，x之后的第一个比它更大的元素，如果不存在，则搜索答案为-1。这意味着你应该循环地搜索它的下一个更大的数。

🚀 示例

🖊️ 题解

模拟

​ 一个最简单的解题做法就是根据题意对整个过程进行模拟：遍历nums数组，在每一轮遍历中，首先查找nums[i]右侧第一个比它大的元素，如果找不到，则向左侧从nums[0]到nums[i-1]查找，如果仍然找不到，则返回-1。

public class Solution {
    public int[] nextGreaterElements(int[] nums) {
        int[] result = new int[nums.length];
        outer:
        for (int i = 0; i < nums.length; i++) {
            for (int j = i + 1; j < nums.length; j++) {
                if (nums[j] > nums[i]) {
                    result[i] = nums[j];
                    continue outer;
                }
            }
            for (int j = 0; j < i; j++) {
                if (nums[j] > nums[i]) {
                    result[i] = nums[j];
                    continue outer;
                }
            }
            result[i] = -1;

        }
        return result;
    }
}

单调栈

​ 根据下一个更大元素 I中单调栈的解法可以得出：要想获取每个元素的下一个更大元素，我们可以轻松地使用反向遍历+维护单调栈的模板算法解决。然而在该题中，由于数组是循环的，因此每个元素的下一个更大元素可能在数组的右侧，也可能在数组的左侧。这就导致在反向遍历中，当前元素nums[i]在被处理时，其左边的元素未被处理。

​ 为了解决以上难点，我们可以将原始数组nums”翻倍“，即在原始数组后拼接一个与其一摸一样的数组。这样一来，在反向遍历数组时，当前nums[i]相当于会被处理两次，在第一次处理时，其右边的元素已被处理，在第二次处理时，其左边的元素也已被处理。

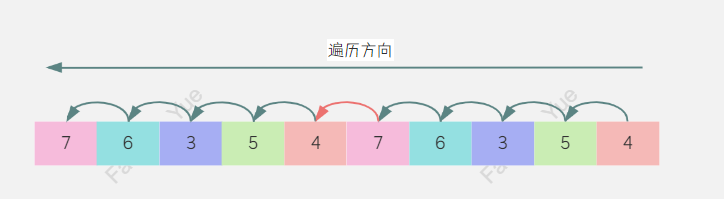
​ 因此，我们可以把这个双倍长度的数组构造出来，然后套用反向遍历 + 维护单调栈的模板算法。但在这里，我们并不这样做，而是根据循环数组的特点来模拟双倍数组。循环数组arr可以通过取余操作实现循环遍历，在反复的循环中，同一个元素的真实下标可以通过index % arr.length获取，其中index为该元素在循环中不断变化的下标。

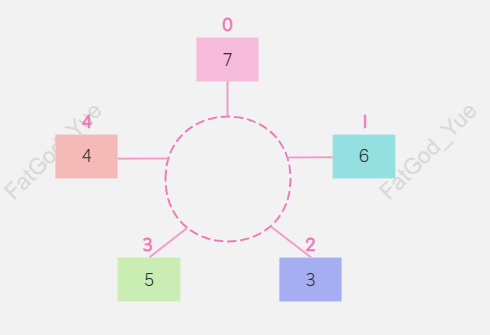
​ 在本题中，我们不需要无限循环地遍历数组nums，而是反向地循环遍历nums两次，并套用反向遍历 + 维护单调栈的模板算法。

public class Solution {
  public int[] nextGreaterElements(int[] nums) {
        int[] results = new int[nums.length];
        Deque<Integer> monotonicStack = new ArrayDeque<>();
        for (int i = nums.length * 2 - 1; i >= 0; i--) {
            int index = i % nums.length;
            while (!monotonicStack.isEmpty() && monotonicStack.peek() <= nums[index]) {
                monotonicStack.pop();
            }
            results[index] = monotonicStack.isEmpty() ? -1 : monotonicStack.peek();
            monotonicStack.push(nums[index]);
        }
        return results;
    }
}

💭 复杂度分析

​ 基于模拟的解决方案的复杂度分析如下。

• 时间复杂度：$O(n^2)$，其中$n$为nums的长度。
• 空间复杂度：$O(1)$ ，返回值不计入空间复杂度。

​ 基于单调栈的解决方案的复杂度分析如下。

• 时间复杂度：$O(n)$，其中$n$为nums的长度。
• 空间复杂度：$O(n)$ 。