📜 设计浏览器历史记录

📝 题目描述

​ 你有一个只支持单个标签页的浏览器，最开始你浏览的网页（主页）是homepage，你可以访问其它的网站url，也可以在浏览历史中后退steps步或前进steps步。

​ 现请你实现一个BrowserHistory类，要求如下。

1. public BrowserHistory(String homepage)是类的初始化方法的签名，homepage表示主页。
2. public void visit(String url)是访问其它网站的方法的签名，用于从当前页跳转访问url对应的页面。执行此操作会把浏览历史中能够前进的记录全部删除，即只能后退。
3. public String back(int steps)是后退方法的签名，用于在浏览历史中后退steps步。如果你只能在浏览历史中后退至多x步且steps > x，那么你只能后退x步。请你返回后退后页面的url。
4. public String forward(int steps)是前进方法的签名，用于在浏览历史中前进steps步。如果你只能在浏览历史中前进至多x步且steps > x，那么你只能前进x步。请你返回前进后页面的url。
5. 前进和后退方法中的steps参数区间皆为$[1,100]$​，且浏览器最多包含5000个历史记录。

​ 以上内容符合的语法规则为java语言，C++语言的BrowserHistory类模板如下。

🚀 示例

输入

BrowserHistory history = new BrowserHistory("http://www.fatgod.cn");
history.visit("https://www.baidu.com");
history.visit("https://cn.vuejs.org/");
history.visit("https://ant.design");
String back1 = history.back(3);
System.out.println(back1);
String forward = history.forward(1);
System.out.println(forward);
history.visit("https://redis.io");
history.visit("https://www.oracle.com");
history.visit("https://spring.io");
String back2 = history.back(2);
System.out.println(back2);

输出

🖊️ 题解

​ 该题可以通过一个「栈」和两个「指针」来解决，具体步骤如下。

1. 实现初始化方法。

   ①创建一个辅助栈。

   ②创建两个指针：pos和top。两者初始值皆为-1，pos用于记录当前页在栈中的位置，top用于记录栈顶的位置。需要注意的是，top的值并不等于栈顶索引，而是栈顶索引加一。

   ③将主页homepage压入栈中，并更新pos和top值。

2. 实现visit方法：将新的url设置在pos索引加一的位置，并更新pos和top的值。需要注意的是，我们没有直接删除历史栈中能够前进的页面记录，而是通过更新top值，在逻辑上将它们从历史中剔除。

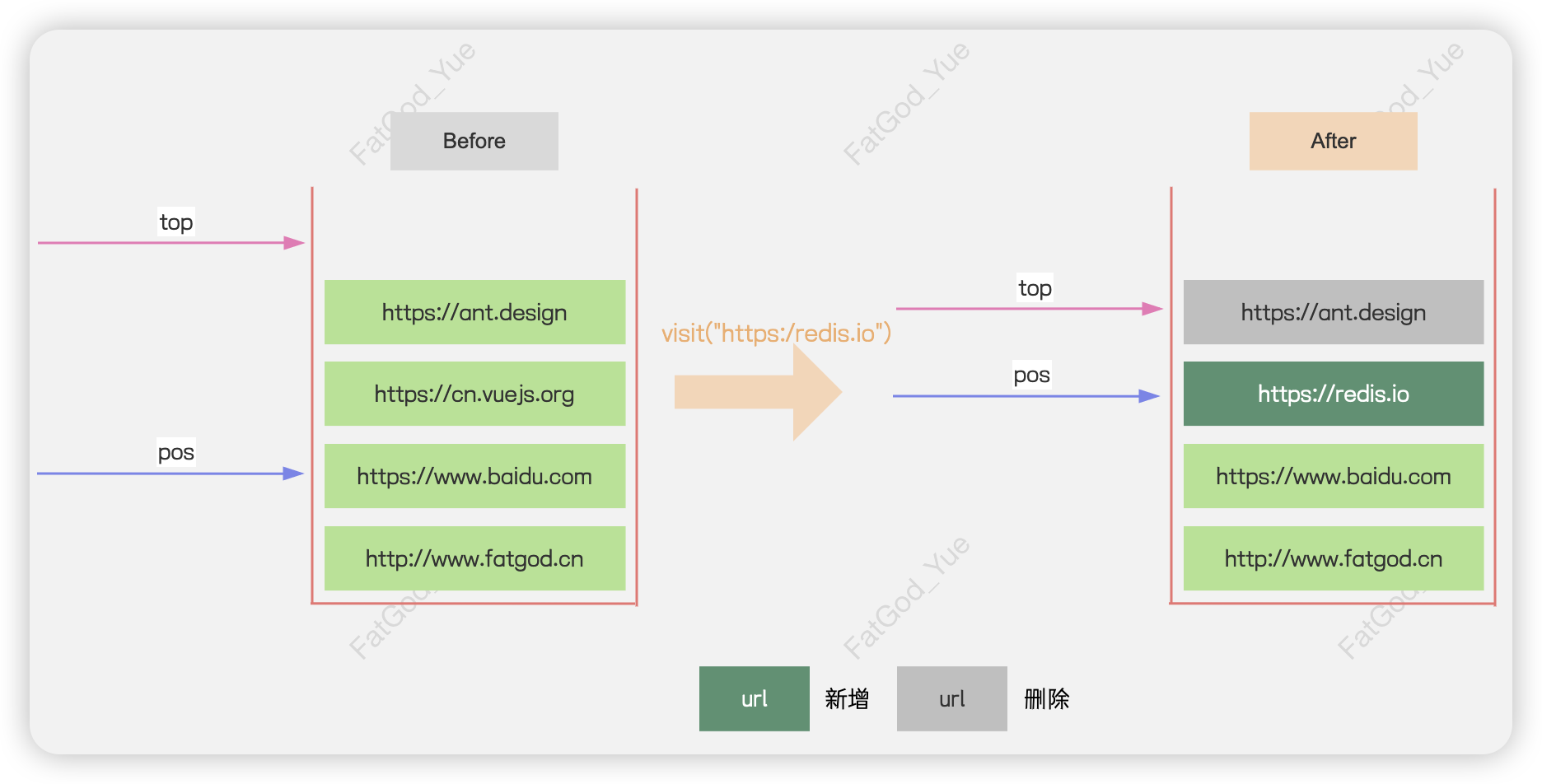
3. 实现back方法：将pos值减去后退的步数，就是后退后返回的页面url，因此只更新pos。需要注意的是，后退步数并不一定等于参数steps，若steps超过了浏览历史至多后退步数x，则取x，否则取steps。

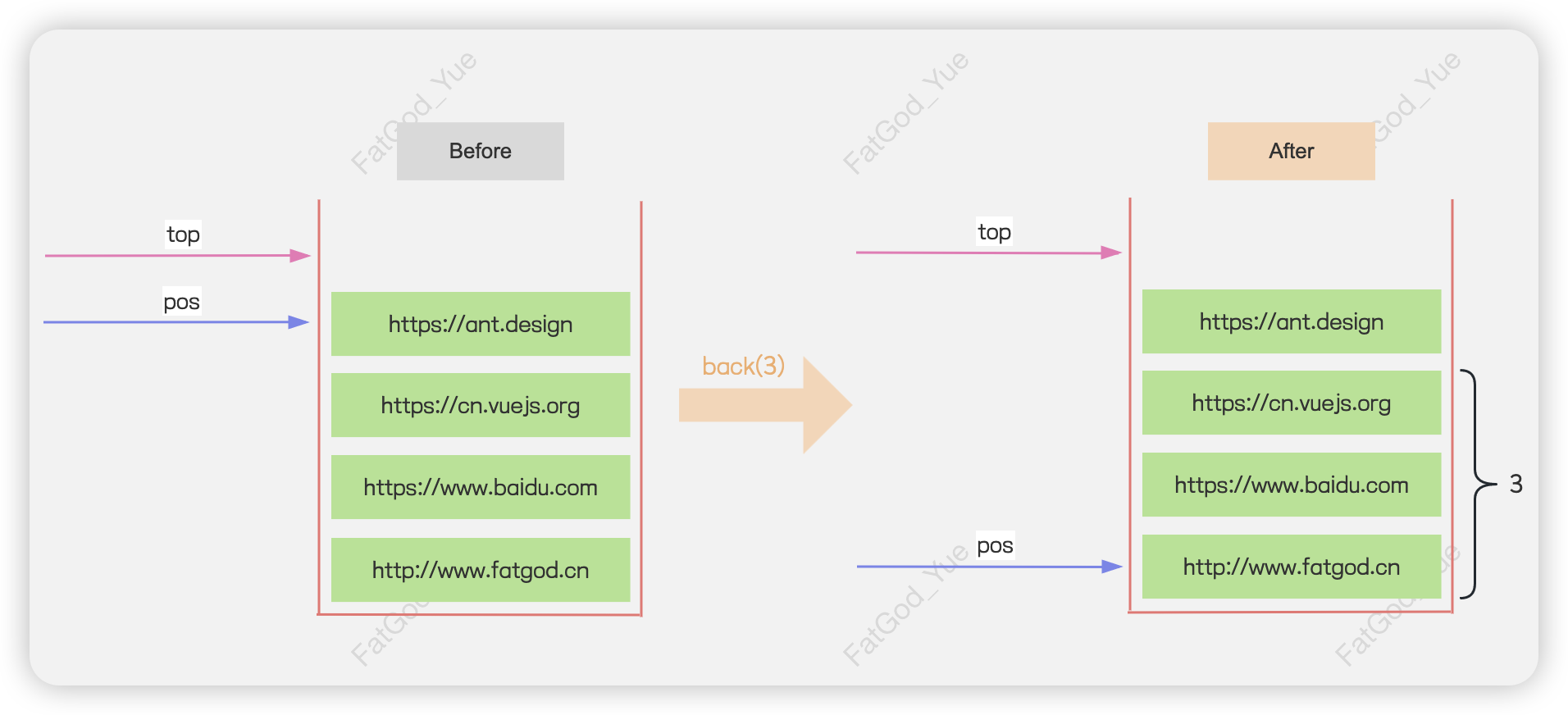
4. 实现forward方法：将pos值加上前进的步数，就是前进后返回的页面url，因此只更新pos。需要注意的是，前进步数并不一定等于参数steps，若steps超过了浏览历史至多前进步数x，则取x，否则取steps。

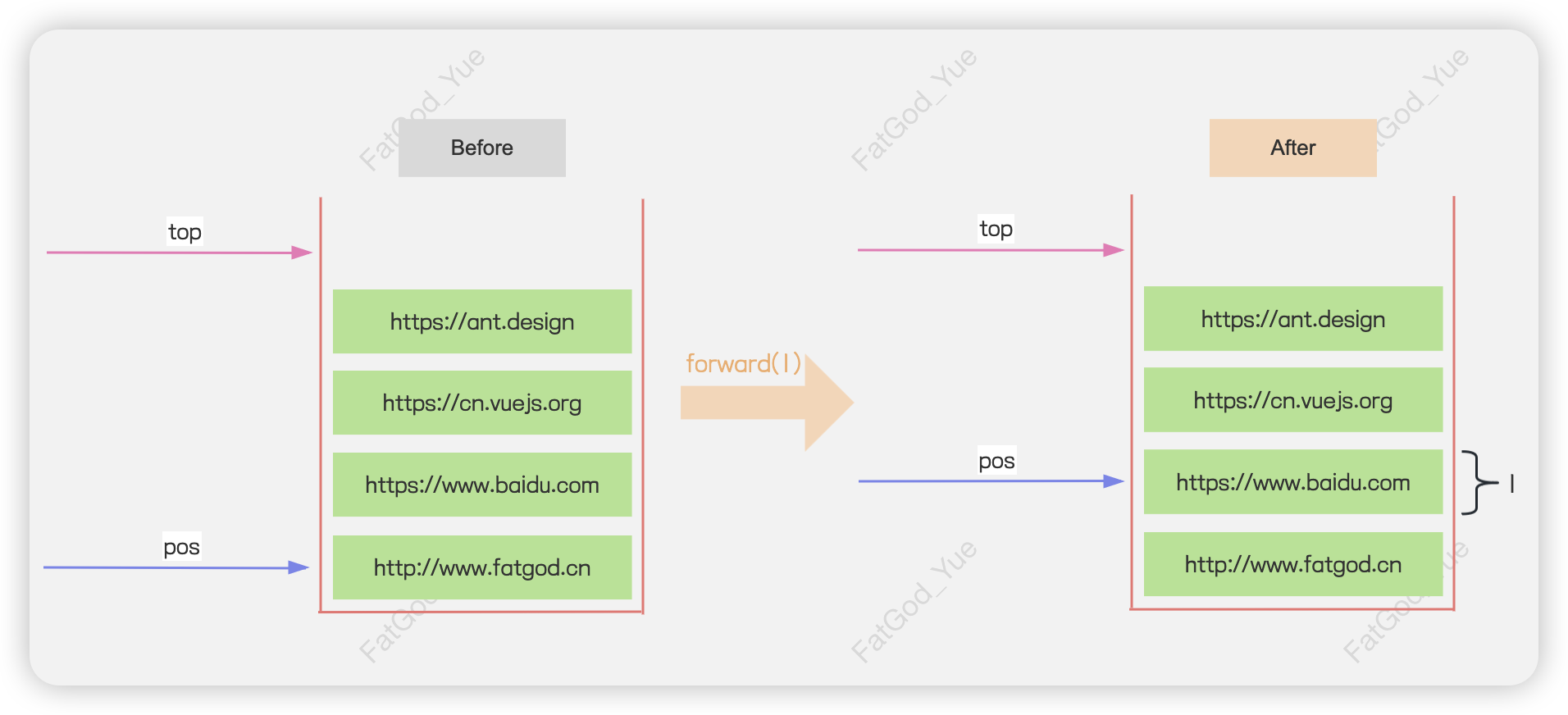
​ ⭐️在BrowserHistory实例初始化时，由于homepage也是压入栈中，并更新pos和top值，因此也直接调用visit方法。

public class BrowserHistory {
    private final ArrayList<String> stack;

    public int top = -1;

    public int pos = -1;

    public BrowserHistory(String homepage) {
        stack = new ArrayList<>(500);
        visit(homepage);
    }

    public void visit(String url) {
        pos++;
        if (stack.size() <= pos) {
            stack.add(url);
        } else {
            stack.set(pos, url);
        }
        top = pos + 1;
    }

    public String back(int steps) {
        int realSteps = Math.min(pos, Math.max(steps, 0));
        pos -= realSteps;
        return stack.get(pos);
    }

    public String forward(int steps) {
        int realSteps = Math.min(top - pos - 1, Math.max(steps, 0));
        pos += realSteps;
        return stack.get(pos);
    }
    
}

💭 复杂度分析

​ 基于栈 + 双指针的解决方案的复杂度分析如下。

• 时间复杂度：不考虑数组扩容，visit、back和forward操作皆为$O(1)$。
• 空间复杂度：$O(n)$。